题目内容
5.已知抛物线y=-(x-1)2+m(m是常数),点A(x1,y1),B(x1,y1)在抛物线上,若x1<1<x2,x1+x2>2,则下列大小比较正确的是( )| A. | m>y1>y2 | B. | m>y2>y1 | C. | y1>y2>m | D. | y2>y1>m |
分析 由解析式可知抛物线开口向下,对称轴为x=1,函数的最大值是m,然后根据x1<1<x2,x1+x2>2,得出x2-1>1-x1,即可判断点A(x1,y1)离对称轴较近,根据与对称轴的远近即可判断y1>y2,
解答 解:由抛物线y=-(x-1)2+m(m是常数)可知抛物线开口向下,对称轴为x=1,由最大值y=m,
∵点A(x1,y1),B(x1,y1)在抛物线上,若x1<1<x2,x1+x2>2,
∴x2-1>1-x1,
∴点A(x1,y1)离对称轴较近,
∴y1>y2,
故m>y1>y2,
故选A.
点评 本题考查了二次函数图象上点的坐标特征:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,则抛物线上的点的坐标满足其解析式;当a<0,抛物线开口向下;对称轴为直线x=-$\frac{b}{2a}$,在对称轴左侧,y随x的增大而增大,在对称轴右侧,y随x的增大而减小.

练习册系列答案
相关题目
16.山东省2014年的快递业务量为1.4亿件,若2016年的快递业务量达到4.5亿件,设这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
13.在实数$\frac{22}{7}$,0,-$\sqrt{2}$,2π中,无理数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.下列方程是一元二次方程的是( )
| A. | x2-1=y | B. | (x+2)(x+1)=x2 | C. | 6x2=0 | D. | x2=$\frac{1}{x}$ |
10.国家卫生和计划生育委员会公布H7N9禽流感病毒直径约为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-9米 | B. | 1.2×10-8米 | C. | 12×10-8米 | D. | 1.2×10-7米 |
17.方程组$\left\{\begin{array}{l}{x+y=2}\\{2x+2y=3}\end{array}\right.$没有解,因此直线y=-x+2和直线y=-x+$\frac{3}{2}$在同一平面直角坐标系中的位置关系是( )
| A. | 重合 | B. | 平行 | ||
| C. | 相交 | D. | 以上三种情况都有可能 |
14.下列计算正确的是( )
| A. | x+x2=x3 | B. | x9÷x3=x3 | C. | x2•x3=x6 | D. | (x3)2=x6 |
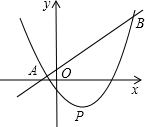 如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A、B两点,抛物线的顶点为P.
如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A、B两点,抛物线的顶点为P.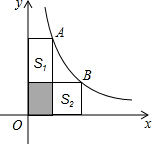 如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.
如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.