题目内容
4. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②③④ | B. | ③④ | C. | ①③④ | D. | ①② |
分析 根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号即可判断①;根据对称轴求出b=-a,即可判断②;求得点(2,0)关于对称轴的对称点为(-1,0),把x=-1代入函数关系式,即可判断③;求出点(0,y1)关于直线x=$\frac{1}{2}$的对称点的坐标,根据对称轴即可判断y1和y2的大小.
解答 解:∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象交y轴的正半轴于一点,
∴c>0,
∵对称轴是直线x=$\frac{1}{2}$,
∴-$\frac{b}{2a}$=$\frac{1}{2}$,
∴b=-a>0,
∴abc<0.
故①正确;
∵由①中知b=-a,
∴a+b=0,
故②正确;
由对称轴为x=$\frac{1}{2}$,点(2,0)的对称点是(-1,0),
∴当x=-1时,y=0,即a-b+c=0.
故③正确;
∵(0,y1)关于直线x=$\frac{1}{2}$的对称点的坐标是(1,y1),
∴y1=y2.
故④正确;
综上所述,正确的结论是①②③④.
故选:A.
点评 本题考查了二次函数的图象和系数的关系的应用,注意:当a>0时,二次函数的图象开口向上,当a<0时,二次函数的图象开口向下.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列计算正确的有( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{\frac{1}{2}}$=2$\sqrt{2}$ |
19.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}\\{x+2y=4}\end{array}\right.$的解满足$x+y>\frac{1}{2}$,则满足条件的m的所有正整数值是( )
| A. | 1,2,3,4 | B. | 1,2,3 | C. | 1,2 | D. | 1 |
9.下列各式中计算正确的是( )
| A. | x2•x4=x6 | B. | 2m-(n+1)=2m-n+1 | C. | x5+2x5=3x10 | D. | (2a)3=2a3 |
16.山东省2014年的快递业务量为1.4亿件,若2016年的快递业务量达到4.5亿件,设这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
13.在实数$\frac{22}{7}$,0,-$\sqrt{2}$,2π中,无理数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.下列计算正确的是( )
| A. | x+x2=x3 | B. | x9÷x3=x3 | C. | x2•x3=x6 | D. | (x3)2=x6 |
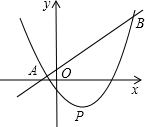 如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A、B两点,抛物线的顶点为P.
如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A、B两点,抛物线的顶点为P.