题目内容
12.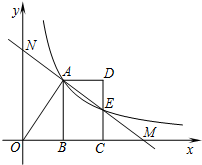 反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC的中点E.
反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC的中点E.(1)求k的值和直线AE的函数表达式;
(2)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.
分析 (1)由已知得,在Rt△OAB中,OB=2,tan∠AOB=$\frac{3}{2}$,求得AB=3,代入y=$\frac{k}{x}$得到k=xy=6,根据已知条件得到点E的纵坐标为$\frac{3}{2}$,由点E在双曲线y=$\frac{k}{x}$(x>0)的图象上,得到点E的坐标为(4,$\frac{3}{2}$),解方程组即可得到结论;
(2)根据y=-$\frac{3}{4}$x+$\frac{9}{2}$求得点M(6,0),N(0,$\frac{9}{2}$),延长DA交y轴于点F,则AF⊥ON,且AF=2,OF=3,根据全等三角形的性质即可得到结论.
解答 解:(1)由已知得,在Rt△OAB中,OB=2,tan∠AOB=$\frac{3}{2}$,
∴AB=3,
∴A点的坐标为(2,3),
∴k=xy=6,
∵DC由AB平移得到,点E为DC的中点,
∴点E的纵坐标为$\frac{3}{2}$,
又∵点E在y=$\frac{k}{x}$(x>0)的图象上,
∴点E的坐标为(4,$\frac{3}{2}$),
设直线MN的函数表达式为y=k1x+b,
则$\left\{\begin{array}{l}2{k_1}+b=3\\ 4{k_1}+b=\frac{3}{2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k_1}=-\frac{3}{4}\\ b=\frac{9}{2}\end{array}\right.$,
∴直线MN的函数表达式为y=-$\frac{3}{4}$x+$\frac{9}{2}$;
(2)结论:AN=ME,
理由:在表达式y=-$\frac{3}{4}$x+$\frac{9}{2}$中,
令y=0可得x=6,令x=0可得y=$\frac{9}{2}$,
∴点M(6,0),N(0,$\frac{9}{2}$),
延长DA交y轴于点F,则AF⊥ON,且AF=2,OF=3,
∴NF=ON-OF=x,∵CM=6-4=2=AF,EC=$\frac{3}{2}$=NF,
在△ANF与△MEC中,$\left\{\begin{array}{l}{AF=CM}\\{∠AFN=∠MCE}\\{FN=CE}\end{array}\right.$,
∴△ANF≌△MEC,
∴AN=ME.
点评 本题考查了全等三角形的判定和性质,待定系数法求函数的解析式,解直角三角形,图形与坐标的性质,求的点E的坐标是解题的关键.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
| A. | -2 | B. | $-\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
| A. | y=(x+1)2-13 | B. | y=(x-5)2-3 | C. | y=(x-5)2-13 | D. | y=(x+1)2-3 |
| A. | 3a+2a=5a2 | B. | a6÷a2=a3 | C. | (-3a3)2=9a6 | D. | (a+2)2=a2+4 |
 某同学进行社会调查,随机抽查了某小区的40户家庭的年收入(万元)情况,并绘制了如图不完整的频数直方图,每组包括前一个边界值,不包括后一个边界值.
某同学进行社会调查,随机抽查了某小区的40户家庭的年收入(万元)情况,并绘制了如图不完整的频数直方图,每组包括前一个边界值,不包括后一个边界值.