题目内容
5．在圆的内接四边形ABCD中，∠A、∠B、∠C的度数之比为2：3：4，则∠D的度数是90°．分析 根据圆内接四边形的性质得到∠A+∠C=∠B+∠D，设∠A，∠B，∠C的度数分别为2x、3x、4x，根据圆内接四边形的性质列出方程，解方程求出x，计算即可．
解答 解：∵四边形ABCD是圆内接四边形，
∴∠A+∠C=∠B+∠D=180°，
设∠A，∠B，∠C的度数分别为2x、3x、4x，
则2x+64=180°，
解得，x=30°，
则∠B=3x=90°，
∴∠D=180°-∠B=90°．
故答案是：90．
点评 本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
15．如图图形是轴对称图形的有（ ）个
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5 |
17．
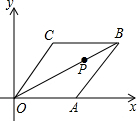已知菱形OABC在平面直角坐标系中的位置如图所示，顶点A在x轴的正半轴上，OB=4$\sqrt{3}$，∠COA═60°，点P是对角线OB上的一个动点，点D的坐标为（0，1），则CP+DP的最小值为（ ）
已知菱形OABC在平面直角坐标系中的位置如图所示，顶点A在x轴的正半轴上，OB=4$\sqrt{3}$，∠COA═60°，点P是对角线OB上的一个动点，点D的坐标为（0，1），则CP+DP的最小值为（ ）| A． | 5 | B． | $\sqrt{17}$ | C． | 4 | D． | $\sqrt{3}$ |
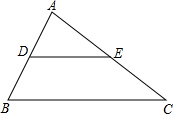如图，在△ABC中，DE∥BC，且S△ADE：S四边形BCED=1：2，BC=26，求DE的长．