题目内容
14．
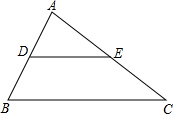如图，在△ABC中，DE∥BC，且S△ADE：S四边形BCED=1：2，BC=26，求DE的长．
分析 由已知S△ADE：S四边形BCED=1：2得S△ADE=$\frac{1}{3}$S△ABC，由DE∥BC得△ADE∽△ABC，根据相似三角形面积比等于相似比的平方，求出对应边$\frac{DE}{BC}$的值，进而得出DE的长．
解答 解：∵S△ADE：S四边形BCED=1：2，
∴S△ADE=$\frac{1}{3}$S△ABC，
∵DE∥BC，
∴△ADE∽△ABC，
∴（$\frac{DE}{BC}$）2=$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$，
∴$\frac{DE}{BC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∵BC=26，
∴DE=$\frac{26\sqrt{3}}{3}$．
点评 本题考查了相似三角形的判定与性质，平行线分线段成比例定理．关键是利用平行线得出相似三角形，利用相似三角形的性质解题．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
2．若m，n为有理数，对于mx=n，下列说法正确的（ ）
| A． | 当m≠0时，为一元一次方程 | B． | 当m=0时，为一元一次方程 | ||
| C． | 当m=0且n≠0时，为一元一次方程 | D． | 当m=0且n=0时，为一元一次方程 |
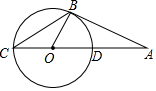如图，AB是⊙O的切线，点C在⊙O上，且AC经过点O，若∠A=20°，AD=2，AB=4．
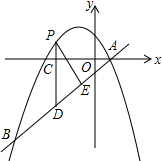如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点，点A在x轴上，点B的横坐标为-8．