题目内容
7.菱形ABCD中,对角线AC、BD交于点O,且AC=2BD,以AD为斜边在菱形ABCD同侧作Rt△ADE.
(1)如图1,当点E落在边AB上时.
①求证:∠BDE=∠BAO;
②求$\frac{DO}{OF}$的值;
③当AF=6时,求DF的长.
(2)如图2,当点E落在菱形ABCD内部,且AE=DE时,猜想OE与OB的数量关系并证明.
分析 (1)①根据菱形的性质和对顶角相等证明即可;
②根据∠BAO=∠ODF以及正切的概念计算;
③设OF=x,根据题意用x表示出OD、AO,根据题意求出x的值,根据勾股定理计算即可;
(2)连结BE,证明△AEO≌△DEB,得到△OEB为等腰直角三角形,即可解答.
解答 解:(1)①∵四边形ABCD是菱形,
∴AC⊥BD,又△ADE是直角三角形,
∴∠AEF=∠DOF=90°,
∴∠BDE+∠DFO=∠BAO+∠AFE,
∵∠AFE=∠DFO,
∴∠BDE=∠BAO;
②∵AC=2BD,
∴AO=2OB,
∴tan∠BAO=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴tan∠ODF=$\frac{OF}{OD}$=$\frac{1}{2}$,
∴$\frac{DO}{OF}$=2;
③设OF=x,则OD=2x,AO=4x,
∵AF=6,
∴4x-x=6,
∴x=2,即OF=2,DO=4,
由勾股定理得,DF=$\sqrt{O{D}^{2}+O{F}^{2}}$=2$\sqrt{5}$;
(2)OB=$\sqrt{2}$OE.
理由如下:如图2,连结BE,
在△AEO和△DEB中,
$\left\{\begin{array}{l}{AE=DE}\\{∠EAO=∠EDB}\\{AO=DB}\end{array}\right.$,
∴△AEO≌△DEB,
∴EO=EB,∠AEO=∠DEB,
∴∠AEO-∠DEO=∠DEB-∠DEO,即∠OEB=∠AED=90°,
∴OB=$\sqrt{2}$OE.
点评 本题考查的是菱形的性质、等腰直角三角形的性质、全等三角形的判定和性质,掌握菱形的四条边相等、对角线互相垂直、灵活运用全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.按照山西省“改薄工程”规划,我省5年投入85亿元用于改造农村县(市、区)薄弱学校,促进义务教育均衡发展,其中某项“改薄工程”建设,甲队单独完成需要20天,若由甲队先做13天,则剩下的工程由甲、乙两队合作3天完成.问乙队单独完成这项工程需要多少天?若设乙队单独完成这项工程需要x天,根据题意可列方程为( )
| A. | 13+3+x=20 | B. | $\frac{13}{20}$+3($\frac{1}{20}$+$\frac{1}{x}$)=1 | C. | $\frac{13}{20}$+$\frac{3}{x}$=1 | D. | (1-$\frac{13}{20}$)+x=3 |
2.2-2的值是( )
| A. | -4 | B. | -2 | C. | 2 | D. | $\frac{1}{4}$ |
16.-8的立方根是( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |
17.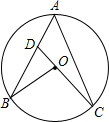 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,四边形DECB的面积是10,则△ABC的面积为( )