题目内容
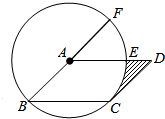 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知 |
| EF |
| π |
| 2 |
考点:切线的性质,平行四边形的性质,扇形面积的计算
专题:
分析:观察可以发现S阴影部分的面积=S△ACD-S扇形ACE,再根据各图形的面积公式,计算出相应的边长求出即可.
解答:
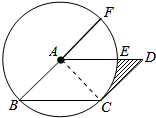 解:连接AC,
解:连接AC,
∵DC是⊙A的切线,
∴AC⊥CD,
又∵AB=AC=CD,
∴△ACD是等腰直角三角形,
∴∠CAD=45°,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CAD=∠ACB=45°,
∠FAE=∠B,
又∵AB=AC,
∴∠ACB=∠B=45°,
∴∠FAD=∠B=45°,
∵
的长为
,
∴
=
,
解得:r=2,
∴S阴影=S△ACD-S扇形ACE=1
2×2×2-
=2-
.
故答案为:2-
.
 解:连接AC,
解:连接AC,∵DC是⊙A的切线,
∴AC⊥CD,
又∵AB=AC=CD,
∴△ACD是等腰直角三角形,
∴∠CAD=45°,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CAD=∠ACB=45°,
∠FAE=∠B,
又∵AB=AC,
∴∠ACB=∠B=45°,
∴∠FAD=∠B=45°,
∵
 |
| EF |
| π |
| 2 |
∴
| π |
| 2 |
| 45πr |
| 180 |
解得:r=2,
∴S阴影=S△ACD-S扇形ACE=1
2×2×2-
| 45π×22 |
| 360 |
| π |
| 2 |
故答案为:2-
| π |
| 2 |
点评:本题主要考查了扇形的面积计算方法,求阴影部分的面积就是将不规则图形的面积转化为规则图形的面积的和或差解决.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、a5+a5=a10 |
| B、a6•a4=a24 |
| C、a100÷a100=1 |
| D、(a4)2=a6 |
 如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.
如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.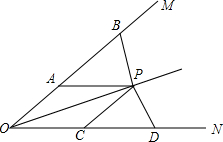 如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD
如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD


