题目内容
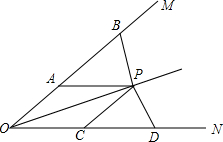 如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD
如图,OP平分∠MON,点A与B,点C与D分别在射线OM、ON上,且AB=CD(1)△ABP与△PCD的面积是否相等?请说明理由.
(2)当OA=OC时,求证:△ABP≌△CDP.
考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)作PG⊥OM于G,PH⊥ON于H,根据角平分线的性质得出PG=PH,然后根据三角形的面积公式即可证得△ABP与△PCD的面积相等;
(2)根据SAS证得△OPB≌△OPD和△OPA≌△OPC分别求得PB=PD,PA=PC,再根据SSS即可证得△ABP≌△CDP.
(2)根据SAS证得△OPB≌△OPD和△OPA≌△OPC分别求得PB=PD,PA=PC,再根据SSS即可证得△ABP≌△CDP.
解答:
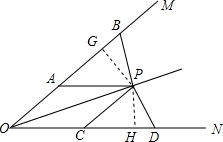 解:(1)作PG⊥OM于G,PH⊥ON于H,
解:(1)作PG⊥OM于G,PH⊥ON于H,
∵OP平分∠MON,
∴PG=PH,
∵S△ABP=
AB•PG,S△PCD=
CD•PH,AB=CD,
∴S△ABP=S△PCD,
所以△ABP与△PCD的面积是否相等;
(2)∵AB=CD,OA=OC,
∴OB=OD,
在△OPB与△OPD中,
,
∴△OPB≌△OPD(SAS),
∴PB=PD,
在△OPA与△OPC中,
,
∴△OPA≌△OPC(SAS),
∴PA=PC,
在△ABP与△CDP中,
,
∴△ABP≌△CDP(SSS).
 解:(1)作PG⊥OM于G,PH⊥ON于H,
解:(1)作PG⊥OM于G,PH⊥ON于H,∵OP平分∠MON,
∴PG=PH,
∵S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABP=S△PCD,
所以△ABP与△PCD的面积是否相等;
(2)∵AB=CD,OA=OC,
∴OB=OD,
在△OPB与△OPD中,
|
∴△OPB≌△OPD(SAS),
∴PB=PD,
在△OPA与△OPC中,
|
∴△OPA≌△OPC(SAS),
∴PA=PC,
在△ABP与△CDP中,
|
∴△ABP≌△CDP(SSS).
点评:本题考查了角平分线的性质,三角形全等的判定和性质,三角形面积等,熟练掌握性质定理是解题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
下列说法正确的是( )
| A、x+y是一次单项式 | ||||
B、多项式3
| ||||
| C、x的系数和次数都是1 | ||||
| D、单项式4×104x2的系数是4 |
 在△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.试说明:CE=BD.
在△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.试说明:CE=BD.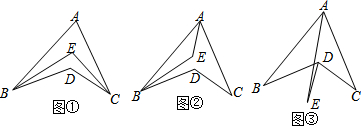
 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.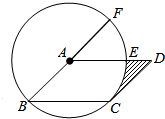 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知