题目内容
13. 如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.
如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.
分析 由DE∥BC,可证△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,求△ABC的面积,再与△ADE的面积作差即可.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=${(\frac{AD}{AB})}^{2}$=${(\frac{1}{1+2})}^{2}$=$\frac{1}{9}$,
∵S△ADE=4cm2,
∴S△ABC=36cm2,
∴四边形BCED的面积为:32cm2,
故答案为:32cm2.
点评 本题考查了相似三角形的判定与性质.关键是利用平行线得相似,利用相似三角形的面积的性质求解.

练习册系列答案
相关题目
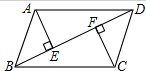 如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
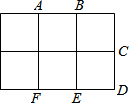 如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10.
如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10.