题目内容
8.(1)计算:(-2)3+2sin30°+|-3|;(2)化简:$\frac{{{x^2}-1}}{{{x^2}-2x+1}}-\frac{2x+2}{x-1}$÷(x+1).
分析 (1)根据绝对值的意义和特殊角的三角函数值得到原式=-8+2×$\frac{1}{2}$+3,然后进行乘法运算后再进行加减运算;
(2)先把分子分母分解因式和除法运算化为乘法运算,再进行约分得到原式=$\frac{x+1}{x-1}$-$\frac{2}{x-1}$,然后进行同分母的减法运算,最后约分得到原式=1.
解答 解:(1)原式=-8+2×$\frac{1}{2}$+3
=-4;
(2)原式=$\frac{(x+1)(x-1)}{(x-1)^{2}}$-$\frac{2(x+1)}{x-1}$•$\frac{1}{x+1}$
=$\frac{x+1}{x-1}$-$\frac{2}{x-1}$
=$\frac{x+1-2}{x-1}$
=1.
点评 本题考查了分式的混合运算:分式的混合运算要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.注意运算的结果要化成最简分式或整式.根据题目的特点,运用乘法的运算律运算,会简化运算过程.也考查了实数的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.函数$y=\frac{x}{{\sqrt{3-2x}}}$中,自变量x的取值范围是( )
| A. | $x<\frac{2}{3}$ | B. | $x<\frac{3}{2}$ | C. | $x≥\frac{2}{3}$ | D. | $x≥\frac{3}{2}$ |
20.点P(4,-2)所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.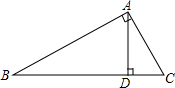 如图所示,下列说法不正确的是( )
如图所示,下列说法不正确的是( )
 如图所示,下列说法不正确的是( )
如图所示,下列说法不正确的是( )| A. | 点B到AC的垂线段是线段AB | B. | 点C到AB的垂线段是线段AC | ||
| C. | 线段AD是点D到AB的垂线段 | D. | 线段BD是点B到AD的垂线段 |
 设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证:
设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证: 如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.
如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.