题目内容
3.因式分解:(1)4x2-4x+1;
(2)16x2-9y2
(3)25+(a+2b)2-10(a+2b)
(4)9(a+b)2-4(a-b)2
(5)(a2+b2)2-4a2b2;
(6)2x2y-8xy+8y;
(7)a2(x-y)+b2(y-x)
(8)(x2-2x)2+2(x2-2x)+1
(9)a4-16;
(10)(x2-1)2+6(1-x2)+9.
(11)81x4-72x2y2+16y4.
分析 (1)原式利用完全平方公式分解即可;
(2)原式利用平方差公式分解即可;
(3)原式利用完全平方公式分解即可;
(4)原式利用平方差公式分解即可;
(5)原式利用平方差公式及完全平方公式分解即可;
(6)原式提取2y,再利用完全平方公式分解即可;
(7)原式变形后,提取公因式,在利用平方差公式分解即可;
(8)原式利用完全平方公式分解即可;
(9)原式利用平方差公式分解即可;
(10)原式利用完全平方公式分解即可;
(11)原式利用完全平方公式分解即可.
解答 解:(1)原式=(2x-1)2;
(2)原式=(4x+3y)(4x-3y);
(3)原式=(a+2b-5)2;
(4)原式=[3(a+b)-2(a-b)][3(a+b)+2(a-b)]=(a+5b)(5a+b);
(5)原式=(a2+b2+2ab)(a2+b2-2ab)=(a+b)2(a-b)2;
(6)原式=2y(x2-4x+4)=2y(x-2)2;
(7)原式=(x-y)(a2-b2)=(x-y)(a+b)(a-b);
(8)原式=(x2-2x+1)2=(x-1)4;
(9)原式=(a2+4)(a2-4)=(a2+4)(a+2)(a-2);
(10)原式=(x2-1+3)2=(x2+2)2;
(11)原式=(9x2-4y2)2=(3x+2y)2(3x-4y)2.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
 如图,在四边形ABCD中,∠A=∠C=90°.
如图,在四边形ABCD中,∠A=∠C=90°.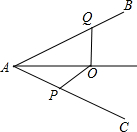 如图,AO是∠BAC的平分线,P、Q分别是AC、AB边上的点,若∠OQB+∠OPC=180°,此时OP与OQ会相等吗?若相等请证明,不相等请说明理由.
如图,AO是∠BAC的平分线,P、Q分别是AC、AB边上的点,若∠OQB+∠OPC=180°,此时OP与OQ会相等吗?若相等请证明,不相等请说明理由.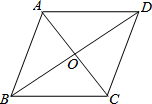 菱形ABCD的两对角线AC、BD长分别为10cm和24cm,它的周长52cm,面积120cm2.
菱形ABCD的两对角线AC、BD长分别为10cm和24cm,它的周长52cm,面积120cm2.