题目内容
8.解答:(1)已知x-2y=2016,求[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷8x;
(2)设y=kx,是否存在实数k,使得对于任意x,y,(x2-y2)(4x2-y2)+3x2(4x2-y2)化简的结果为0?若存在,请求出所有满足条件的k的值;若不存在,请说明理由.
分析 (1)把原式利用整式的乘法法则和乘法公式进行化简,把给出的值整体代入计算即可;
(2)运用提公因式法把原式因式分解,根据平方根的概念解答即可.
解答 解:(1)[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷8x
=(9x2-4y2-5x2-8xy+4y2)÷8x
=(4x2-8xy)÷8x
=$\frac{x-2y}{2}$,
当x-2y=2016时,原式=1008;
(2)(x2-y2)(4x2-y2)+3x2(4x2-y2)
=(4x2-y2)(4x2-y2)
=(4x2-y2)2,
当4x2-y2=0,即y=±2x时,原式化简结果为0,
∴k的值为±2.
点评 本题考查的是整式的化简求值,掌握整式的乘法法则和乘法公式是解题的关键,注意整体思想的应用和平方根的概念的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一个五次单项式的系数为1,且同时含有字母a、b、c,那么这样的单项式有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
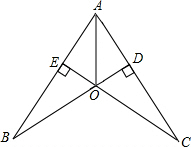 已知:如图,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且BO=CO,求证:O在∠BAC的角平分线上.
已知:如图,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且BO=CO,求证:O在∠BAC的角平分线上.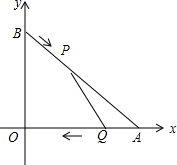 如图,A,B两点的坐标分别是(8,0),(0,6),点P由点B出发沿BA方向向点A做匀速直线运动,速度为每秒3个单位长度,同时,点Q由A出发沿AO(O为坐标原点)方向向点O做匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒,解答如下问题:设△AQP的面积为S个平方单位,求S与t之间的函数关系式,并求出S的最大值.
如图,A,B两点的坐标分别是(8,0),(0,6),点P由点B出发沿BA方向向点A做匀速直线运动,速度为每秒3个单位长度,同时,点Q由A出发沿AO(O为坐标原点)方向向点O做匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒,解答如下问题:设△AQP的面积为S个平方单位,求S与t之间的函数关系式,并求出S的最大值.