题目内容
7. 已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.
已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.
分析 过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N,根据角平分线上的点到角的两边距离相等可得PD=PM,同理可得PM=PN,从而得到PD=PN,再根据到角的两边距离相等的点在角的平分线上证明即可.
解答  证明:如图,过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N,
证明:如图,过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N,
∵BE平分∠ABC,点P在BE上,
∴PD=PM,
同理,PM=PN,
∴PD=PN,
∴点P在∠A的平分线上.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
2.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表(单位:环):
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
12. 已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )
已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )
 已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )
已知a、b、c在数轴上的位置如图所示,试化简|a+b|-|b|+|b+c|+|c|的结果是( )| A. | a+b | B. | a+b-2c | C. | -a-b-2c | D. | a+b+2c |
17.已知2x2+y=1,x2-xy=2,则3x2+y(1-x)-1=( )
| A. | 4 | B. | -1 | C. | 3 | D. | 2 |
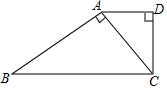 如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度.
如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度. 在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来:
在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来: 用一段长30米的篱笆围成一个一边靠墙的矩形花圃,墙长为18米,另三边用篱笆恰好围成.围成的花圃是如图的矩形ABCD.设AB边的长为x米,花圃ABCD的面积为S平方米,则S与x之间的函数关系式是s=x(30-2x).(不必写出自变量取值范围)
用一段长30米的篱笆围成一个一边靠墙的矩形花圃,墙长为18米,另三边用篱笆恰好围成.围成的花圃是如图的矩形ABCD.设AB边的长为x米,花圃ABCD的面积为S平方米,则S与x之间的函数关系式是s=x(30-2x).(不必写出自变量取值范围)