题目内容
12．
已知a、b、c在数轴上的位置如图所示，试化简|a+b|-|b|+|b+c|+|c|的结果是（ ）| A． | a+b | B． | a+b-2c | C． | -a-b-2c | D． | a+b+2c |
分析 根据数轴上右边的数总是大于左边的数即可判断a、b、c的符号和大小，根据绝对值的性质即可去掉绝对值符号，然后合并同类项即可．
解答 解：根据数轴可得b＜c＜0＜a，且|a|＜|b|
则a+b＜0，b+c＜0．
则原式=-（a+b）+b-（b+c）-c
=-a-b+b-b-c-c
=-a-b-2c．
故选C．
点评 本题考查了利用数轴比较数的大小，右边的数总是大于左边的数，以及绝对值的性质，正确根据性质去掉绝对值符号是关键．
练习册系列答案
名校课堂系列答案
相关题目
3．以下代数式书写规范的是（ ）
| A． | （a+b）÷2 | B． | $\frac{6}{5}$y | C． | 1$\frac{1}{3}$x | D． | x+y厘米 |
P为等边△ABC内的一点，PA=10，PB=6，PC=8，将△ABP绕点B顺时针旋转60°到△CBP′位置．
已知：如图，△ABC的角平分线BE、CF相交于点P．求证：点P在∠A的平分线上．
17．
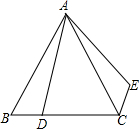如图，△ABC是等边三角形，D为BC边上的点，△ABD绕点A沿逆时针方向旋转后到达△ACE的位置，那么旋转了（ ）
如图，△ABC是等边三角形，D为BC边上的点，△ABD绕点A沿逆时针方向旋转后到达△ACE的位置，那么旋转了（ ）| A． | 75° | B． | 60° | C． | 45° | D． | 15° |