题目内容
分解因式：4m3n－16mn3.
4mn(m＋2n)(m－2n)
【解析】试题分析：提取公因式4mn后，再利用平方差公式因式分解即可.
试题解析：
4m3n－16mn3
=4mn(m2－4n2)
=4mn(m＋2n)(m－2n).
练习册系列答案
相关题目
如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角等于（ ）
A. 55° B. 70° C. 125° D. 145°
C
【解析】试题分析：∵∠B=35°，∠C=90°，∴∠BAC=90°﹣∠B=90°﹣35°=55°，∵点C、A、B1在同一条直线上，
∴∠BAB′=180°﹣∠BAC=180°﹣55°=125°，∴旋转角等于125°．
故选C． 已知：如图，点C在线段AB上，以AC和BC为边在AB的同侧作正三角形△ACM和△BCN，连结AN、BM，分别交CM、CN于点P、Q．求证：PQ∥AB．
见解析
【解析】试题分析：首先证明△ACN≌△MCB可得∠ANC=∠MBC，再证明△PCN≌△QCB可得PC=QC，再有∠MCN=60°可得△PCQ是等边三角形，进而得到∠PQC=60°，可证明PQ∥AB．
试题解析：∵△ACM和△BCN都是正三角形，
∴∠ACM=∠BCN=60°，AC=CM，BC=CN.
∵点C在线段AB上，
∴∠ACM=∠BCN=∠MCN=60°... 已知等腰三角形的一个角为75°，则其顶角为（ ）.
A. 30° B. 75° C. 105° D. 30°或75°
D
【解析】试题分析：因为等腰三角形的一个角为75°，没有明确说明是底角还是顶角，所以要分两种情况进行分析．
【解析】
当75°角为底角时，顶角为180°﹣75°×2=30°；
75°角为顶角时，其底角==52.5°，
所以其顶角为30°或75°．
故选D． 一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 计算1052－952的结果为( )
A. 1000 B. 1980
C. 2000 D. 4000
C
【解析】1052－952=（105+95）（105-95）=200×10=2000，故选C. 二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），... 如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
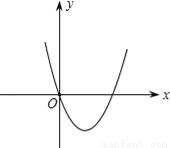
A. a=﹣1 B. a=
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
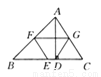
故选C． 如图所示，△ABC中AD⊥BC，E，F，G分别为BC，AB，AC的中点．求证四边形DEFG是等腰梯形．
答案见解析
【解析】试题分析：因为G，F分别是AB，AC的中点，所以GF∥DE，则四边形DEFG是梯形．在Rt△ABD中，G为AB的中点，则DG=AB．而E，F分别是BC，AC的中点，则EF=AB，所以DG=EF，所以四边形DEFG是等腰梯形．
试题解析：证明：∵G，F分别是AB，AC的中点，∴GF∥DE，易得EF不平行于DG，∴四边形DEFG是梯形．在Rt△ABD中，G为AB的中点，...