题目内容
将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm．
优质课堂快乐成长系列答案今年，6月12日为端午节．在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况．请根据小丽提供的信息，解答小华和小明提出的问题．
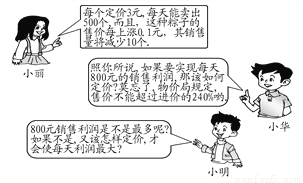
(1)当定价为4元时，能实现每天800元的销售利润(2)当定价为4.8元时，每天的销售利润最大．
【解析】试题分析：（1）小华的问题要用一元二次方程来解决，解答的关键是弄清：设实现每天800元利润的定价为x元/个时，每一个粽子的利润为（x-2）元，一共能卖（500-×10）个粽子，根据题意列方程得：（x-2)（500-×10）=800，解得x1=4,x2=6，还应根据实际问题确定两个值是否都... 如图，在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小芳距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米.
0.5
【解析】试题分析：首先以点名所在的直线为x轴，最低点所在的直线为y轴建立平面直角坐标系，然后求出二次函数的解析式，最后计算出顶点坐标，顶点坐标的纵坐标就是距离地面的距离. 线段AB沿和它垂直的方向平移到A′B′，则线段AB和线段A′B′的位置关系是__．
平行且相等
【解析】【解析】
∵线段AB沿和它垂直的方向平移到A′B′，∴线段AB和线段A′B′的位置关系是平行且相等．故答案为：平行且相等． 如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角等于（ ）
A. 55° B. 70° C. 125° D. 145°
C
【解析】试题分析：∵∠B=35°，∠C=90°，∴∠BAC=90°﹣∠B=90°﹣35°=55°，∵点C、A、B1在同一条直线上，
∴∠BAB′=180°﹣∠BAC=180°﹣55°=125°，∴旋转角等于125°．
故选C． 已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件．市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．
（1）求w与x之间的函数关系式，并写出自变量x的取值范围；
（2）该产品销售价定为每件多少元时，每星期的销售利润最大？最大利润是多少元？
（3）该产品销售价在什么范围时，每星期的销售利润不低于6000元，请直接写出结果．
（1）w=﹣20x2+100x+6000，x≤4，且x为整数；（2）售价不低于56元且不高于60元时，每星期利润不低于6000元．
【解析】试题分析：（1）根据利润=（售价﹣进价）×销售件数即可求得W与x之间的函数关系式；
（2）利用配方法求得函数的最大值，从而可求得答案；
（3）根据每星期的销售利润不低于6000元列不等式求解即可．
试题解析: （1）w=（20﹣x）（3... 抛物线y=x2﹣5x+6与x轴交于A、B两点，则AB的长为__．
1
【解析】试题分析：当y=0，则0=x2﹣5x+6，
解得：x1=2，x2=3，
故AB的长为：3﹣2=1． 如图，在等腰△ABC中，∠A=80°，∠B和∠C的平分线相交于点O
（1）连接OA，求∠OAC的度数；
（2）求：∠BOC。
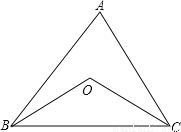
(1) 40°;(2) 130°
【解析】试题分析：（1）连接AO，利用等腰三角形的对称性即可求得∠OAC的度数；（2）利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系，再把∠A代入即可求∠BOC的度数．
试题解析：
（1）连接AO，
∵在等腰△ABC中，∠B和∠C的平分线相交于点O，
∴等腰△ABC关于线段AO所在的直线对称，
∵∠A=80°，
... 计算1052－952的结果为( )
A. 1000 B. 1980
C. 2000 D. 4000
C
【解析】1052－952=（105+95）（105-95）=200×10=2000，故选C.