题目内容
4．给出下列命题：①一组对边和一组对角分别相等的四边形是平行四边形；②两组对角的内角平分线分别平行的四边形是平行四边形；③一组对边中点间的距离等于另一组对边长和的一半的四边形是平行四边形；④两条对角线都平分四边形的面积的四边形是平行四边形．其中真命题有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据平行四边形的5种判定方法一一判断即可．
解答 解：①一组对边相等，一组对角相等的四边形，不能证明另一组对边也相等或平行，即一组对边和一组对角分别相等的四边形不一定是平行四边形，故①错误；
②两组对角的内角平分线分别平行的四边形，能证明两组对角相等，故四边形一定是平行四边形，故②正确；
③一组对边中点的距离等于另一组对边边长的和的一半的四边形，梯形中两腰中点的连线也可以符合等于上下底的一半，故③错误；
④两条对角线都平分四边形的面积的四边形是平行四边形，可以推出两组对边之间的距离相等，可证明两组对边平行，故④正确；
故正确的有②④．
故选B．
点评 此题主要考查了平行四边形的判定，关键是通过给定的条件推可判定四边形是平行四边形的条件，平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法
练习册系列答案
相关题目
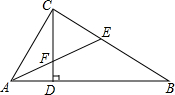如图所示，在△ABC中，∠ACB=90°，高CD和角平分线AE交于点F，求证：CF=CE．