题目内容
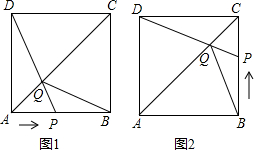 如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.
如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.(1)如图1,当点P在AB边上运动时.①求证:△ADQ≌△ABQ;
②若AP=n,当n为何值时,△ADQ的面积是正方形ABCD面积的
| 1 |
| 6 |
(2)如图1、2,若记点P运动所经过的路程为x,求使得△BPQ为等腰三角形时x的值.
考点:四边形综合题
专题:
分析:(1)①根据四边形ABCD是正方形,得出AD=AB,∠DAQ=∠BAQ,再根据AQ=AQ即可证出△ADQ≌△ABQ;
②根据S△ADQ=
S正方形ABCD,得出AQ:AC=1:3,AQ:CQ=1:2,再求出AP:CD=1:2,最后根据CD=1,求出AP=
,即可得出答案;
(2)分两种情况讨论:
①当点P在边AB上时,要使△BPQ为等腰三角形,则∠PBQ=∠PQB,得出2∠ADQ+∠ADQ=90°,∠ADQ=30°,即可求出AP=x=
;
②当点P在BC边上时,先求出CP=
,从而得出x=2-
.
②根据S△ADQ=
| 1 |
| 6 |
| 1 |
| 2 |
(2)分两种情况讨论:
①当点P在边AB上时,要使△BPQ为等腰三角形,则∠PBQ=∠PQB,得出2∠ADQ+∠ADQ=90°,∠ADQ=30°,即可求出AP=x=
| ||
| 3 |
②当点P在BC边上时,先求出CP=
| ||
| 3 |
| ||
| 3 |
解答:(1)①证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAQ=∠BAQ=45°,
在△ADQ和△ABQ中,
,
∴△ADQ≌△ABQ(SAS);
②解:若S△ADQ=
S正方形ABCD,S△ADQ=
S△ACD,
则AQ:AC=1:3,AQ:CQ=1:2,
∵AB∥CD,
∴△APQ∽△CDQ,
∴AP:CD=AQ:CQ=1:2,
∵CD=1,
∴AP=
,
∴n=
,
∴当n=
时,△ADQ的面积是正方形ABCD面积的
.
(2)解:①当点P在边AB上时,
∵∠BPQ>90°,要使△BPQ为等腰三角形,必须PB=PQ
∴∠PBQ=∠PQB,
∴∠APQ=2∠ABQ=2∠ADQ
∴2∠ADQ+∠ADQ=90°
∴∠ADQ=30°
∴AP=x=
;
②当点P在BC边上时,由①易知CP=
,
∴x=2-
;
综上①②,当x=
或2-
时,△BPQ为等腰三角形.
∴AD=AB,∠DAQ=∠BAQ=45°,
在△ADQ和△ABQ中,
|
∴△ADQ≌△ABQ(SAS);
②解:若S△ADQ=
| 1 |
| 6 |
| 1 |
| 3 |
则AQ:AC=1:3,AQ:CQ=1:2,
∵AB∥CD,
∴△APQ∽△CDQ,
∴AP:CD=AQ:CQ=1:2,
∵CD=1,
∴AP=
| 1 |
| 2 |
∴n=
| 1 |
| 2 |
∴当n=
| 1 |
| 2 |
| 1 |
| 6 |
(2)解:①当点P在边AB上时,
∵∠BPQ>90°,要使△BPQ为等腰三角形,必须PB=PQ
∴∠PBQ=∠PQB,
∴∠APQ=2∠ABQ=2∠ADQ
∴2∠ADQ+∠ADQ=90°
∴∠ADQ=30°
∴AP=x=
| ||
| 3 |
②当点P在BC边上时,由①易知CP=
| ||
| 3 |
∴x=2-
| ||
| 3 |
综上①②,当x=
| ||
| 3 |
| ||
| 3 |
点评:此题考查了四边形综合,用到的知识点是等腰三角形全等三角形的性质与判定、正方形的性质,关键是综合运用有关性质得出有关结论,注意分类讨论思想的运用.

练习册系列答案
相关题目
化简
+
的值为( )
| 8-a |
| -a2 |
A、
| ||||
B、
| ||||
C、3
| ||||
D、2
|
不等式组
的解集是( )
|
| A、x>1 | B、x>-1 |
| C、-1<x<1 | D、-3<x<1 |
 在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(| 7 |
| 2 |
| 3 |
| 2 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|

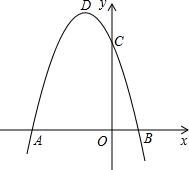 如图,在平面直角坐标系中抛物线y=kx2+2kx-3k(k<0)与x轴交于A,B两点,与y轴交于点C,点D是抛物线的顶点.
如图,在平面直角坐标系中抛物线y=kx2+2kx-3k(k<0)与x轴交于A,B两点,与y轴交于点C,点D是抛物线的顶点.