题目内容
如图①,双曲线y=
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(-1,-3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求
的值.

| k |
| x |
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求
| DN |
| NB |

考点:二次函数综合题
专题:代数几何综合题
分析:(1)用待定系数法即可求得.
(2)过O作OM⊥BC,则OM=
,因为OB=
,根据勾股定理求得MB=2
,进而求得tan∠COM=
=
=2,所以tan∠POE=2,从而求得P点的坐标.
(3)根据勾股定理求得DF、OB的长,根据DF∥OB得出
=
即可求得.
(2)过O作OM⊥BC,则OM=
| 2 |
| 10 |
| 2 |
| BM |
| OM |
2
| ||
|
(3)根据勾股定理求得DF、OB的长,根据DF∥OB得出
| DN |
| NB |
| DF |
| OB |
解答:解:(1)∵抛物线y=ax2+bx(a≠0)过B(3,1),C(-1,-3),
∴
,
解得:
,
∴抛物线的解析式为:y=-
x2+
x,
把B(3,1)代入y=
(k≠0)得:1=
,
解得:k=3,
∴双曲线的解析式为:y=
.
(2)存在点P,使得∠POE+∠BCD=90°;
∵B(3,1),C(-1,-3),设直线BC为y=kx+n,
∴
,
解得k=1,n=-2,
∴直线BC为:y=x-2,
∴直线BC与坐标轴的交点(2,0),(0,-2),
过O作OM⊥BC,则OM=
,
∵B(3,1),C(-1,-3),
∴OB=OC=
,
∴BM=
=
=2
,
∴tan∠COM=
=
=2,
∵∠COM+∠BCD=90°,∠POE+∠BCD=90°,
∴∠POE=∠COM,
∴tan∠POE=2,
∵P点是抛物线上的点,设P(m,-
m2+
m),
∴
=2,
解得:m=
,
∴P(
,1).
综上所述,存在点P(
,1),使得∠POE+∠BCD=90°.
(3)∵直线CO过C(-1,-3),
∴直线CO的解析式为y=3x,
解
,
解得
,
∴D(1,3),
∵B(3,1),
∴直线OB的斜率=
,
∵直线l⊥OB,过点D作DF⊥l于点F,
∴DF∥OB,
∴直线l的斜率=-3,直线DF的斜率=
,
∵直线l过B(3,1),直线DF过D(1,3),
∴直线l的解析式为y=-3x+10,直线DF解析式为y=
x+
,
解
,
解得
,
∴F(
,
),
∴DF=
=
,
∵DF∥OB,OB=
,
∴△DNF∽△BNO,
∴
=
=
=
.
∴
|
解得:
|
∴抛物线的解析式为:y=-
| 2 |
| 3 |
| 7 |
| 3 |
把B(3,1)代入y=
| k |
| x |
| k |
| 3 |
解得:k=3,
∴双曲线的解析式为:y=
| 3 |
| x |
(2)存在点P,使得∠POE+∠BCD=90°;
∵B(3,1),C(-1,-3),设直线BC为y=kx+n,
∴
|

解得k=1,n=-2,
∴直线BC为:y=x-2,
∴直线BC与坐标轴的交点(2,0),(0,-2),
过O作OM⊥BC,则OM=
| 2 |
∵B(3,1),C(-1,-3),
∴OB=OC=
| 10 |
∴BM=
| OB2-OM2 |
| 10-2 |
| 2 |
∴tan∠COM=
| BM |
| OM |
2
| ||
|
∵∠COM+∠BCD=90°,∠POE+∠BCD=90°,
∴∠POE=∠COM,
∴tan∠POE=2,
∵P点是抛物线上的点,设P(m,-
| 2 |
| 3 |
| 7 |
| 3 |
∴
-
| ||||
| m |
解得:m=
| 1 |
| 2 |
∴P(
| 1 |
| 2 |
综上所述,存在点P(
| 1 |
| 2 |
(3)∵直线CO过C(-1,-3),
∴直线CO的解析式为y=3x,
解
|
解得
|
∴D(1,3),
∵B(3,1),
∴直线OB的斜率=
| 1 |
| 3 |
∵直线l⊥OB,过点D作DF⊥l于点F,
∴DF∥OB,
∴直线l的斜率=-3,直线DF的斜率=
| 1 |
| 3 |
∵直线l过B(3,1),直线DF过D(1,3),
∴直线l的解析式为y=-3x+10,直线DF解析式为y=
| 1 |
| 3 |
| 8 |
| 3 |
解
|
解得
|
∴F(
| 11 |
| 5 |
| 17 |
| 5 |
∴DF=
(
|
| 2 |
| 5 |
| 10 |
∵DF∥OB,OB=
| 10 |
∴△DNF∽△BNO,
∴
| DN |
| NB |
| DF |
| OB |
| ||||
|
| 2 |
| 5 |
点评:本题考查了待定系数法求解析式,勾股定理的运用,平行线的斜率的特点,以及图象的交点等.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若关于x的不等式mx-n>0的解集是x<
,则关于x的不等式(m+n)x>n-m的解集是( )
| 1 |
| 5 |
A、x<-
| ||
B、x>-
| ||
C、x<
| ||
D、x>
|
下列命题中,真命题是( )
| A、相等的角是对顶角 |
| B、同旁内角互补 |
| C、平行于同一条直线的两条直线互相平行 |
| D、垂直于同一条直线的两条直线互相垂直 |
若a<b,下列变形正确的是( )
| A、a-5>b-5 | ||||
B、-
| ||||
| C、2a>2b | ||||
| D、a+3<b+3 |
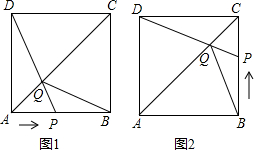 如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.
如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.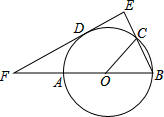 如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.
如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.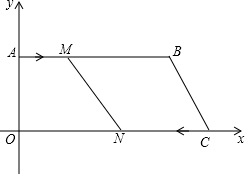 如图,在平面直角坐标系中,四边形AOCB的点O在坐标原点上,点A在y轴上,AB∥OC,点B的坐标为(15,8),点C的坐标为(21,0),动点M从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M、N同时出发,一点到达终点时,另一点也停止运动,设运动时间为t秒.
如图,在平面直角坐标系中,四边形AOCB的点O在坐标原点上,点A在y轴上,AB∥OC,点B的坐标为(15,8),点C的坐标为(21,0),动点M从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M、N同时出发,一点到达终点时,另一点也停止运动,设运动时间为t秒.