题目内容
9.已知方程|x-a|+|x+a|=a有解,那么有理数a的值是( )| A. | 0 | B. | 1 | C. | -1 | D. | 不能确定 |
分析 根据绝对值的性质分情况讨论,即可求出答案.
解答 解:由于|x-a|+|x+a|≥0,
∴a≥0,
当x≤-a时,
∴原方程化为:-(x-a)-(x+a)=a,
解得:x=-$\frac{a}{2}$,此时-$\frac{a}{2}$>-a,不符合题意,
当-a<x<a时,
∴原方程化为:-(x-a)+x+a=a,
∴a=0,符合题意,
当x≥a时,
原方程化为:x-a+x+a=a,
∴2x=a,
∴x=$\frac{a}{2}$,此时$\frac{a}{2}$≥a,不符合题意,
综上所述,有理数a的值是0,
故选A.
点评 本题考查了带有字母系数和绝对值的一元一次方程的解,根据绝对值的意义将绝对值化去,可以解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.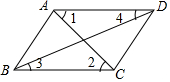 如图,下列条件中,不能判定AD∥BC的是( )
如图,下列条件中,不能判定AD∥BC的是( )
 如图,下列条件中,不能判定AD∥BC的是( )
如图,下列条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ADC+∠DCB=180° | D. | ∠BAD+∠ADC=180° |
20.已知a、b、c是△ABC的三边长,且|a-3|+(4-b)2+$\sqrt{c-5}$=0,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
17.如果△ABC三边a、b、c满足(a-4)2+$\sqrt{b-3}$+|c-5|=0,那么△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
4.三角形的三边长a,b,c满足关系式(a+2b-60)2+|b-18|+$\sqrt{c-30}$=0,则这个三角形是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
14.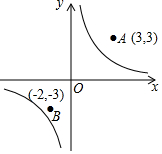 反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
 反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )
反比例函数的图象如图所示,则这个反比例函数的解析式可能是( )| A. | y=$\frac{2}{x}$ | B. | y=$\frac{6}{x}$ | C. | y=$\frac{7}{x}$ | D. | y=$\frac{9}{x}$ |
1.下列计算正确的是( )
| A. | ($\sqrt{6}$)2=±6 | B. | ($\sqrt{-7}$)2=-7 | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=3 |
18.下列说法正确的是( )
| A. | 投掷质量分布均匀的六面体骰子600次,骰子六面分别标有1,2,3,4,5,6,那么出现5点的机会大约为100次 | |
| B. | 抛掷硬币实验中,抛掷500次和抛掷1000次没什么区别 | |
| C. | 现有9张卡片,分别标有1至9这九个数字,将它们背面朝上洗匀后,任意抽出一张,因小丽的幸运数是“8”,所以她抽到数字8的机会比抽到其他数字的机会大 | |
| D. | 某彩票的中奖机会是1%,买1张一定不会中奖 |
19.宜昌市高新区计划到2016年实现总收入4500亿元,这个数据用科学记数法表示为( )元.
| A. | 4.5×1011 | B. | 4.5×103 | C. | 4.5×1012 | D. | 45×104 |