题目内容
1.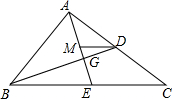 如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.
如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.
分析 由线段AE、BD是△ABC的中线,得到BE=CE,AD=CD,根据DM∥BC,得到AM=ME,求得DM=$\frac{1}{2}$CE=$\frac{1}{2}$BE,通过△DMG∽△BEG,得到$\frac{MG}{EG}=\frac{DM}{BE}$=$\frac{1}{2}$,S△BGE:S△DMG=4:1,求得AM:MG=3:1,推出S△ADM:S△DMG=3:1,即可得到结论.
解答 解:∵线段AE、BD是△ABC的中线,
∴BE=CE,AD=CD,
∵DM∥BC,
∴AM=ME,
∴DM=$\frac{1}{2}$CE=$\frac{1}{2}$BE,
∵DM∥BC,
∴△DMG∽△BEG,
∴$\frac{MG}{EG}=\frac{DM}{BE}$=$\frac{1}{2}$,S△BGE:S△DMG=4:1,
∴AM:MG=3:1,
∴S△ADM:S△DMG=3:1,
∴S△AMD=3S△DMG,
∴△AMD,△DMG和△BEG的面积之比为:3:1:4.
故答案为:3:1:4.
点评 本题考查了相似三角形的判定和性质,三角形面积,三角形中线,知道同高不同底的三角形的面积的比等于底的比是解题的关键.

练习册系列答案
相关题目
16.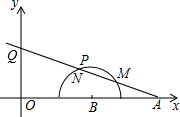 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | $\frac{8}{15}$$\sqrt{3}$ | C. | 2-$\frac{4}{5}$$\sqrt{3}$ | D. | 2$\sqrt{3}$-2 |
13.下列变形正确的是( )
| A. | $\frac{m}{n}=\frac{{m}^{2}}{{n}^{2}}$ | B. | $\frac{2}{5+y}=\frac{2x}{5x+y}$ | ||
| C. | $\frac{-x}{x-y}=\frac{x}{-x+y}$ | D. | $\frac{x+0.23y}{0.5x-y}=\frac{x-23y}{50x-y}$ |
 某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.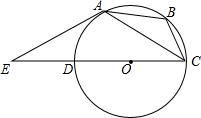 如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC.
如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC.