题目内容
2．生活中，有人喜欢把传送的便条折成如图的形状，折叠过程是这样的（阴影部分表示纸条的反面）：为了美观，人们希望纸条两端超出点P的长度相等（即AP=MB），若纸条的长为26cm，纸条的宽为2cm，则在开始折叠时起点M与点A的距离为10cm．
分析 将折叠纸条展开，分析其中的三角形，梯形的特点，再进行计算．
解答 解：将折叠这条展开如图，
根据折叠的性质可知，两个梯形的上底等于纸条宽，即2cm，
下底等于纸条宽的2倍，即4cm，
两个三角形都为等腰直角三角形，
斜边为纸条宽的2倍，即4cm，
故超出点P的长度为（26-10）÷2=8，
AM=8+2=10cm，
故答案为：10．
点评 本题考查了折叠的性质．关键是将折叠图形展开，分析每个图形形状及与纸条宽的关系．
练习册系列答案
中考解读考点精练系列答案
相关题目
13．下列变形正确的是（ ）
| A． | $\frac{m}{n}=\frac{{m}^{2}}{{n}^{2}}$ | B． | $\frac{2}{5+y}=\frac{2x}{5x+y}$ | ||
| C． | $\frac{-x}{x-y}=\frac{x}{-x+y}$ | D． | $\frac{x+0.23y}{0.5x-y}=\frac{x-23y}{50x-y}$ |
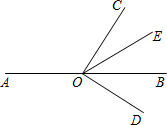如图，O是直线AB上一点，∠COD是直角，OE平分∠BOC．