题目内容
13.有一个计算程序,每次运算都是把一个数先乘以3,再除以它与1的和,多次重复进行这种运算的过程如下:
则第n次的运算结果是yn=$\frac{{3}^{n}x}{(1+3+{3}^{2}+…+{3}^{n-1})x+1}$.(用含字母x和n的代数式表示).
分析 将y1代入y2计算表示出y2,将y2代入y3计算表示出y3,归纳总结得到一般性规律即可得到结果.
解答 解:将y1=$\frac{3x}{x+1}$代入得:y2=$\frac{3×\frac{3x}{x+1}}{\frac{3x}{x+1}+1}$=$\frac{{3}^{2}x}{4x+1}$;
将y2=$\frac{{3}^{2}x}{4x+1}$代入得:y3=$\frac{3×\frac{{3}^{2}x}{4x+1}}{\frac{{3}^{2}x}{4x+1}+1}$=$\frac{{3}^{3}x}{13x+1}$,
依此类推,第n次运算的结果yn=$\frac{{3}^{n}x}{(1+3+{3}^{2}+…+{3}^{n-1})x+1}$.
故答案为:yn=$\frac{{3}^{n}x}{(1+3+{3}^{2}+…+{3}^{n-1})x+1}$=$\frac{{3}^{n}x}{\frac{{3}^{n}-1}{2}x+1}$.
点评 此题考查数字的变化规律,从特殊到一般找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
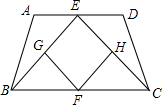 如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形.
如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形. 如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$.
如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$.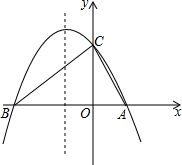 如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$
如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$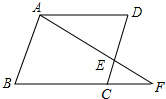 如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.
如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.