题目内容
3.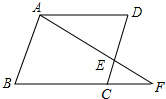 如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.
如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.
分析 在平行四边形ABCD中,由AB∥DC,于是得到△CEF∽△BAF,求得比例式$\frac{CE}{AB}=\frac{CF}{FB}$,代入数据即可得到结论.
解答 解:在平行四边形ABCD中,∵AB∥DC,
∴△CEF∽△BAF,∴$\frac{CE}{AB}=\frac{CF}{FB}$,
∵BC=AD=b,∴$\frac{m}{a}=\frac{CF}{b+CF}$,
∴CF=$\frac{mb}{a-m}$,
∴BF=BC+CF=$\frac{ab}{a-b}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,在⊙O中,∠ABC=40°,则∠AOC=( )度.
如图,在⊙O中,∠ABC=40°,则∠AOC=( )度.
 如图,在⊙O中,∠ABC=40°,则∠AOC=( )度.
如图,在⊙O中,∠ABC=40°,则∠AOC=( )度.| A. | 40 | B. | 20 | C. | 80 | D. | 50 |


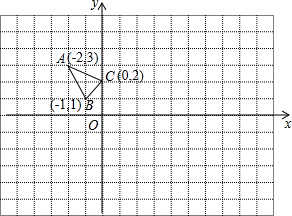 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.
 如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π).
如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π). 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).