题目内容
已知abc=1,则关于x的方程
+
+
=2012的解为 .
| x |
| 1+a+ab |
| x |
| 1+b+bc |
| x |
| 1+c+ac |
考点:对称式和轮换对称式
专题:
分析:根据abc=1,可以得到ab=
,bc=
,代入
,
进行化简,即可求得(
+
+
)的值,从而求解.
| 1 |
| c |
| 1 |
| ab |
| 1 |
| 1+a+ab |
| 1 |
| 1+b+bc |
| 1 |
| 1+a+ab |
| 1 |
| 1+b+bc |
| 1 |
| 1+c+ac |
解答:解:∵abc=1,
∴ab=
,bc=
,
∴
=
=
,
=
=
,
∴
=
,
∴关于x的方程
+
+
=2012即(
+
+
)x=2012,
即(
+
+
)x=2012,
x=2012,
∴x=2012.
故答案是:x=2012.
∴ab=
| 1 |
| c |
| 1 |
| a |
∴
| 1 |
| 1+a+ab |
| 1 | ||
1+a+
|
| c |
| 1+c+ac |
| 1 |
| 1+b+bc |
| 1 | ||
1+b+
|
| a |
| 1+a+ab |
∴
| 1 |
| 1+b+bc |
| ac |
| 1+c+ac |
∴关于x的方程
| x |
| 1+a+ab |
| x |
| 1+b+bc |
| x |
| 1+c+ac |
| 1 |
| 1+a+ab |
| 1 |
| 1+b+bc |
| 1 |
| 1+c+ac |
即(
| c |
| 1+c+ac |
| ac |
| 1+c+ac |
| 1 |
| 1+c+ac |
| 1+c+ac |
| 1+c+ac |
∴x=2012.
故答案是:x=2012.
点评:本题考查了方程的解法,正确求得
+
+
的值是关键.
| 1 |
| 1+a+ab |
| 1 |
| 1+b+bc |
| 1 |
| 1+c+ac |

练习册系列答案
相关题目
 如图,长方形内有两个相邻的正方形,面积分别是m2和9. 那么阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别是m2和9. 那么阴影部分的面积为( )| A、3(m-3) |
| B、(m-3)2 |
| C、m(m-3) |
| D、m2-9 |
 如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC,CD于点E,F.
如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC,CD于点E,F.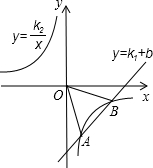 如图,已知一次函数y=k1x+b的图象与反比例函数y=
如图,已知一次函数y=k1x+b的图象与反比例函数y=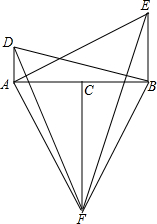 如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.
如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.