题目内容
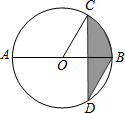 如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4
如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4| 3 |
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
考点:扇形面积的计算
专题:
分析:首先证明OE=
OC=
OB,则可以证得△OEC≌△BED,则S阴影=S扇形OCB,利用扇形的面积公式即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:∵∠COB=2∠CDB=60°,
解:∵∠COB=2∠CDB=60°,
又∵CD⊥AB,
∴∠OCB=30°,CE=DE,
∴OE=
OC=
OB=2
,OC=4.
∴OE=BE,
则在△OEC和△BED中,
,
∴△OEC≌△BED,
∴S阴影=S扇形OCB=
=
.
故选B.
 解:∵∠COB=2∠CDB=60°,
解:∵∠COB=2∠CDB=60°,又∵CD⊥AB,
∴∠OCB=30°,CE=DE,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴OE=BE,
则在△OEC和△BED中,
|
∴△OEC≌△BED,
∴S阴影=S扇形OCB=
| 60π×42 |
| 360 |
| 8π |
| 3 |
故选B.
点评:本题考查了扇形的面积公式,证明△OEC≌△BED,得到S阴影=S扇形OCB是本题的关键.

练习册系列答案
相关题目
 如图,长方形内有两个相邻的正方形,面积分别是m2和9. 那么阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别是m2和9. 那么阴影部分的面积为( )| A、3(m-3) |
| B、(m-3)2 |
| C、m(m-3) |
| D、m2-9 |
如果六条直线两两相交,仅有三条直线过一点,则截得不重复线段有( )条.
| A、42 | B、46 | C、48 | D、50 |
 如图,在平面直角坐标系中,四边形ABCD是正方形,请计算该正方形的面积.
如图,在平面直角坐标系中,四边形ABCD是正方形,请计算该正方形的面积.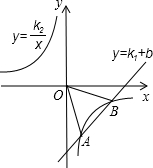 如图,已知一次函数y=k1x+b的图象与反比例函数y=
如图,已知一次函数y=k1x+b的图象与反比例函数y=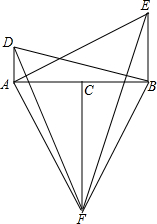 如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.
如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.