题目内容
16.某校九年级共有1100名学生参加“二诊”考试,随机抽取50名学生进行总成绩统计,其中有20名学生总成绩达到优秀,估计这次“二诊”考试总成绩达到优秀的人数大约为( )| A. | 400 | B. | 420 | C. | 440 | D. | 460 |
分析 随机抽取的50名学生的成绩是一个样本,可以用这个样本的优秀率去估计总体的优秀率,从而求得该校九年级学生在这次测试中达到优秀的人数.
解答 解:随机抽取了50名学生的成绩进行统计,共有20名学生成绩达到优秀,
∴样本优秀率为:20÷50=40%,
又∵某校九年级共1100名学生参加“二诊”考试,
∴该校这次“二诊”考试总成绩达到优秀的人数大约为:1100×40%=440人.
故选C.
点评 本题考查了用样本估计总体,这是统计的基本思想,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.计算:(a2b)3的结果是( )
| A. | a6b | B. | a6b3 | C. | a5b3 | D. | a2b3 |
1.点A与点B关于x轴对称,点B与点C关于原点对称,若点A的坐标是($\frac{x-a}{|x-a|}$,$\frac{2x-b}{\sqrt{4{x}^{2}-4bx+{b}^{2}}}$)($\frac{b}{2}$<x<a),则点C的坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
8.有一列数a1、a2、a3、…an,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=-1,则a2013=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 2012 |
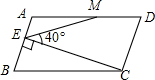 如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°. 如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC.
如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC. 如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.
如图,已知AB与CD交于点O,且△AOC≌△BOD,求证:AC∥BD.