题目内容
4．
如图，△ABC∽△DBE，点E在AC上，∠ABC=∠DBE=90°，连接AD，求证：AD⊥AC．
分析 根据相似三角形的判定定理证明△DBA∽△EBC，根据相似三角形的性质得到∠DAB=∠C，得到答案．
解答 证明：∵∠ABC=∠DBE=90°，
∴∠DBA=∠BCE，
∵△ABC∽△DBE，
∴$\frac{DB}{AB}$=$\frac{BE}{BC}$，即$\frac{DB}{BE}$=$\frac{AB}{AC}$，又∠DBA=∠BCE，
∴△DBA∽△EBC，
∴∠DAB=∠C，
∴∠DAC=90°，即AD⊥AC．
点评 本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．
练习册系列答案
相关题目
14．
如图，P是⊙O外动点，PA，PB，CD是⊙O的三条切线，C，D分别在PA，PB上，连接OC，OD，设∠P为x°，∠COD为y°，则y与x之间的函数关系式为y=90-$\frac{1}{2}$x．
如图，P是⊙O外动点，PA，PB，CD是⊙O的三条切线，C，D分别在PA，PB上，连接OC，OD，设∠P为x°，∠COD为y°，则y与x之间的函数关系式为y=90-$\frac{1}{2}$x． 
如图，在△ABC中，AB=AC=BC=6，求△ABC外接圆⊙O的半径r．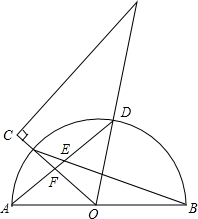
如图，半圆O中，将一块含60°的直角三角板的60°角顶点与圆心O重合，角的两条边分别与半圆圆弧交于C，D两点（点C在∠AOD内部），AD与BC交于点E，AD与OC交于点F．