题目内容
18.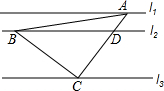 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )| A. | $\frac{4\sqrt{2}}{5}$ | B. | $\frac{\sqrt{34}}{5}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{20\sqrt{2}}{23}$ |
分析 先作出作BF⊥l3,AE⊥l3,再判断△ACE≌△CBF,求出CE=BF=3,CF=AE=4,然后由l2∥l3,求出DG,即可.
解答 解:如图,作BF⊥l3,AE⊥l3,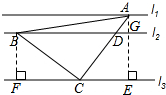
∵∠ACB=90°,
∴∠BCF+∠ACE=90°,
∵∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
在△ACE和△CBF中,
$\left\{\begin{array}{l}{∠BFC=∠CEA}\\{∠CBF=∠ACE}\\{BC=AC}\end{array}\right.$,
∴△ACE≌△CBF,
∴CE=BF=3,CF=AE=4,
∵l1与l2的距离为1,l2与l3的距离为3,
∴AG=1,BG=EF=CF+CE=7
∴AB=$\sqrt{B{G}^{2}+A{G}^{2}}$=5$\sqrt{2}$,
∵l2∥l3,
∴$\frac{DG}{CE}=\frac{AG}{AE}$=$\frac{1}{4}$
∴DG=$\frac{1}{4}$CE=$\frac{3}{4}$,
∴BD=BG-DG=7-$\frac{3}{4}$=$\frac{25}{4}$,
∴$\frac{AB}{BD}=\frac{5\sqrt{2}}{\frac{25}{4}}$=$\frac{4\sqrt{2}}{5}$.
故选A.
点评 此题是平行线分线段成比例试题,主要考查了全等三角形的性质和判定,平行线分线段成比例定理,勾股定理,解本题的关键是构造全等三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.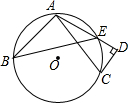 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )| A. | $\frac{7}{12}$ | B. | $\frac{7}{24}$ | C. | $\frac{24}{25}$ | D. | $\frac{16}{25}$ |
8.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线经过点(2,3) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
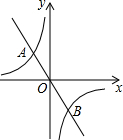 如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.
如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.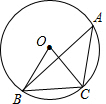 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.