题目内容
7.在括号内填上适当的整式.使下列等式成立:(1)$\frac{x+y}{2}$=$\frac{()}{2x-2y}$;
(2)$\frac{-2x}{1-2x}$=$\frac{()}{2{x}^{2}-x}$;
(3)$\frac{x-y}{2a}$=$\frac{(y-x)^{2}}{()}$.
分析 (1)根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案;
(2)根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案;
(3)根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案.
解答 解:(1)分子分母都乘以(x-y),得
$\frac{x+y}{2}$=$\frac{{x}^{2}-{y}^{2}}{2x-2y}$;
(2)分子分母都乘以(-x),得
$\frac{-2x}{1-2x}$=$\frac{2{x}^{2}}{2{x}^{2}-x}$;
(3)分子分母都乘以(x-y),得
$\frac{x-y}{2a}$=$\frac{(x-y)^{2}}{2ax-2ay}$=$\frac{(y-x)^{2}}{2ax-2ay}$,
故答案为:x2-y2;2x2;2ax-2ay.
点评 本题考查了分式的性质,分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.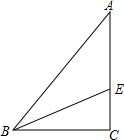 如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )
如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )
 如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )
如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )| A. | 9 | B. | 18 | C. | 15 | D. | 30 |
15.若a<b,则|b-a+1|-|a-b|等于( )
| A. | -1 | B. | 1 | C. | -2a+2b+1 | D. | 2a-2b-1 |
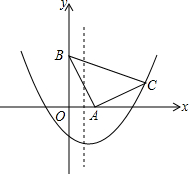 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的解析式.
如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的解析式.