Question

12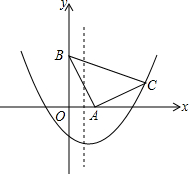．如图，在平面直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=x²+bx-2过点C．求抛物线的解析式．

Answer 1

分析 首先构造全等三角形△AOB≌△CDA，求出点C的坐标；然后利用点C的坐标求出抛物线的解析式．

解答 解：如图1所示，过点C作CD⊥x轴于点D，则∠CAD+∠ACD=90°．
∵∠OBA+∠OAB=90°，∠OAB+∠CAD=90°，
∴∠OAB=∠ACD，∠OBA=∠CAD．
在△AOB与△CDA中，
$\left\{\begin{array}{l}{∠OAB=∠ACD}\\{AB=AC}\\{∠OBA=∠CAD}\end{array}\right.$，
∴△AOB≌△CDA（ASA）．
∴CD=OA=1，AD=OB=2，
∴OD=OA+AD=3，
∴C（3，1）．
∵点C（3，1）在抛物线y=$\frac{1}{2}$x²+bx-2上，
∴1=$\frac{1}{2}$×9+3b-2，解得：b=-$\frac{1}{2}$．
∴抛物线的解析式为：y=$\frac{1}{2}$x²-$\frac{1}{2}$x-2．

点评 本题考查了待定系数法求二次函数的解析式，等腰三角形的性质，三角形全等的判定和性质，作出辅助线构建全等三角形是解题的关键．