题目内容
18.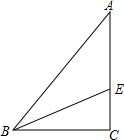 如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )
如图,在Rt△ABC中,BF平分∠ABC交AC于E,已知AB=10,BC=6,AC=8,求△ABE的面积( )| A. | 9 | B. | 18 | C. | 15 | D. | 30 |
分析 作EH⊥AB于H,根据勾股定理的逆定理证明∠C=90°,根据角平分线的性质得到EH=EC,根据三角形的面积公式计算求出EH的长即可.
解答 解: 作EH⊥AB于H,
作EH⊥AB于H,
∵AB=10,BC=6,AC=8,
∴∠C=90°,
∵BF平分∠ABC,∠C=90°,EH⊥AB,
∴EH=EC,
∴$\frac{1}{2}$×AB×EH+$\frac{1}{2}$×BC×EC=$\frac{1}{2}$×AC×BC,
解得,EH=3,
∴△ABE的面积=$\frac{1}{2}$×AB×EH=15,
故选:C.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知$\frac{mn}{3m-n}$=3,那么$\frac{2mn}{3m-n}$+$\frac{6m-2n}{mn}$的值为( )
| A. | 2 | B. | 3 | C. | $\frac{14}{3}$ | D. | $\frac{20}{3}$ |
3.已知二次函数y=3(x-1)2+k的图象上有三点A($\sqrt{2}$,y1),B(2,y2),C(-3,y3),则y1、y2、y3的大小关系为( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
10.已知★×(20152016-20162015)=0,则对★表述错误的是( )
| A. | ★的相反数是自身 | B. | ★的绝对值是自身 | C. | ★的倒数是自身 | D. | ★的4次幂是自身 |
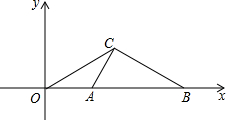 如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.
如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.