题目内容
3.一元二次方程3x2+4x=0的解是x1=0,x2=-$\frac{4}{3}$.分析 提取公因式x,将原式化为两式相乘的形式,再根据“两式相乘值为0,这两式中至少有一式值为0”来解题.
解答 解:提公因式得,x(3x+4)=0,
x=0,或3x+4=0,
解得x1=0,x2=-$\frac{4}{3}$.
故答案为x1=0,x2=-$\frac{4}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
14.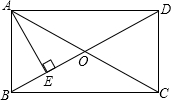 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )| A. | 6 | B. | 5 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
18.已知:m,x,y满足
①$\frac{2}{3}$(x-5)2+8|m|=0;
②-2a2by+1与9b3a2是同类项.
求代数式:2x2-6y2+m(xy-9y2)-(3x2-3xy+7y2)的值.
①$\frac{2}{3}$(x-5)2+8|m|=0;
②-2a2by+1与9b3a2是同类项.
求代数式:2x2-6y2+m(xy-9y2)-(3x2-3xy+7y2)的值.
8.下面四个图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.下列各式中,能用完全平方公式分解因式的是( )
| A. | m2-m+$\frac{1}{4}$ | B. | a2+b2 | C. | a2-2ab-b2 | D. | -25+a2 |
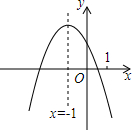 二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)
二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)