题目内容
13.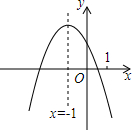 二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)
二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)
分析 由抛物线与x轴有两个交点得到b2-4ac>0;根据对称轴是x=-1,可得x=-2、0时,y的值相等,所以4a-2b+c>0;根据-$\frac{b}{2a}$=-1,得出b=2a,再根据a+b+c<0,可得$\frac{1}{2}$b+b+c<0,所以3b+2c<0,根据抛物线开口判断a<0,然后根据对称轴判断b<0,抛物线交y轴于正半轴,c>0,可得abc>0,据此判断即可.
解答 解:∵图象与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,
∴4ac-b2<0,①正确;
∵当x=-2时,y>0,
∴4a-2b+c>0,
∴4a+c>2b,②错误;
∴-$\frac{b}{2a}$=-1,
∴b=2a,
∵a+b+c<0,
∴$\frac{1}{2}$b+b+c<0,3b+2c<0,
∴③是正确;
∵抛物线开口向下,
∴a<0;
∵抛物线的对称轴为x=-$\frac{b}{2a}$=-1,b=2a,故b<0;
抛物线交y轴于正半轴,得:c>0;
∴abc>0;④正确.
故答案为①③④.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

练习册系列答案
相关题目
4.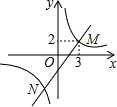 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
8.在下列常见的手机软件小图标中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.解决下列问题,比较容易用普查方式的是( )
| A. | 了解菏泽市中小学生近视率 | B. | 了解菏泽市初中生体育中考的成绩 | ||
| C. | 了解菏泽居民的人均收入情况 | D. | 了解某一天离开菏泽市的人口数量 |
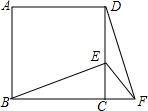 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
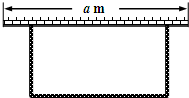 若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.
若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.