题目内容
14.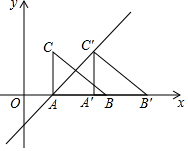 如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )
如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )| A. | (5,3) | B. | (3,5) | C. | (6,4) | D. | (4,6) |
分析 先根据勾股定理求出AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,再由平移的性质得出A′C′=AC=3.把A(2,0)代入y=x+b,求出b=-2,再把y=3代入y=x-2,解得x=5,即可求出点C′的坐标.
解答 解:∵点A、B的坐标分别为(2,0),(6,0),
∴AB=6-2=4,
∵AC⊥x轴,BC=5,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∵将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),
∴A′C′=AC=3.
∵直线y=x+b经过点A(2,0),
∴2+b=0,解得b=-2,
∵直线y=x-2经过点C′,
∴把y=3代入y=x-2,解得x=5,
∴点C′的坐标为(5,3).
故选A.
点评 本题考查了一次函数图象上点的坐标特征,勾股定理,坐标与图形变化-平移,求出点C′的纵坐标以及b的值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知抛物线y=ax2+bx+c(a<0)过A(-4,1),B(0,1),C(x1,y1),D(x2,y2)四点,且y1<y2,则x1与x2的取值可能是( )
| A. | x1=-1,x2=1 | B. | x1=-5,x2=1 | C. | x1=3,x2=-3 | D. | x1=1,x2=-6 |
2.已知一次函数y=(m-1)x+1的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1<y2,那么m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m>-1 | D. | m<-1 |
19.已知一次函数y=-x+1的图象上三个点的坐标分别是A(-2,y1),B(-1,y2),C(2,y3),则能正确反映y1、y2、y3的大小关系的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y2>y3>y1 |
3.下列说法正确的是( )
| A. | “任意一个三角形的外角和等于180°”这一事件是不可能事件 | |
| B. | 必然事件发生的概率为0 | |
| C. | 一组数据1,6,3,9,8的极差为7 | |
| D. | “面积相等的两个三角形全等”这一事件是必然事件 |
4.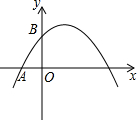 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
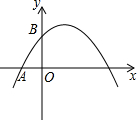 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )| A. | a=-3 | B. | y2<4 | C. | |x1-x2|=1 | D. | |x1-$\frac{3}{2}$|>|x2-$\frac{3}{2}$| |
 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.