题目内容
9. 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
分析 (1)解直角三角形求得AB,作CE⊥OB于E,根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标,然后根据待定系数法即可求得反比例函数的解析式;
(2)求得D的坐标,进而求得AD的长,得出△ACD的面积,然后根据S四边形CDBO=S△AOB-S△ACD即可求得.
解答 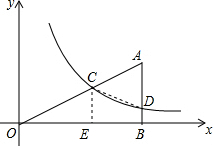 解:(1)∵∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,
解:(1)∵∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,
∴AB=$\frac{\sqrt{3}}{3}$OB=4,
作CE⊥OB于E,
∵∠ABO=90°,
∴CE∥AB,
∴OC=AC,
∴OE=BE=$\frac{1}{2}$OB=2$\sqrt{3}$,CE=$\frac{1}{2}$AB=2,
∴C(2$\sqrt{3}$,2),
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,
∴2=$\frac{k}{2\sqrt{3}}$,
∴k=4$\sqrt{3}$,
∴反比例函数的关系式为y=$\frac{4\sqrt{3}}{x}$;
(2)∵OB=4$\sqrt{3}$,
∴D的横坐标为4$\sqrt{3}$,
代入y=$\frac{4\sqrt{3}}{x}$得,y=1,
∴D(4$\sqrt{3}$,1),
∴BD=1,
∵AB=4,
∴AD=3,
∴S△ACD=$\frac{1}{2}$AD•BE=$\frac{1}{2}$×3×2$\sqrt{3}$=3$\sqrt{3}$,
∴S四边形CDBO=S△AOB-S△ACD=$\frac{1}{2}$OB•AB-3$\sqrt{3}$=$\frac{1}{2}$×4$\sqrt{3}$×4-3$\sqrt{3}$=5$\sqrt{3}$.
点评 本题考查待定系数法求反比例函数的解析式,解决本题的关键是明确反比例函数图象上点的坐标特征.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
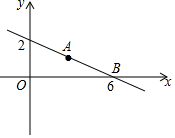 如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6.
如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6.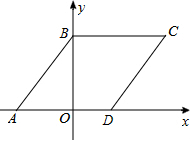 如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(-3,0),(0,4),点D在x轴正半轴上.
如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(-3,0),(0,4),点D在x轴正半轴上. 已知二次函数y=ax2+2ax+a-1(a>0).
已知二次函数y=ax2+2ax+a-1(a>0).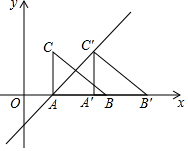 如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )
如图,平面直角坐标系中,△ABC的两个顶点A、B的坐标分别为(2,0),(6,0),AC⊥x轴,BC=5,将△ABC沿x轴向右平移,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标为( )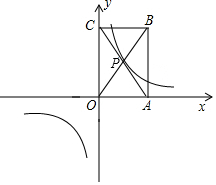 阅读理解:实数a>0,b>0,∵($\sqrt{a}$-$\sqrt{b}}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,即a+b≥2$\sqrt{ab}$.若ab=m(m为定值),则a+b≥2$\sqrt{m}$,当且仅当a=b时等式成立,即a=b时,a+b=2$\sqrt{m}$,∴当a=b=$\sqrt{m}$时,a+b取得最小值(填“最大”或“最小”).
阅读理解:实数a>0,b>0,∵($\sqrt{a}$-$\sqrt{b}}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,即a+b≥2$\sqrt{ab}$.若ab=m(m为定值),则a+b≥2$\sqrt{m}$,当且仅当a=b时等式成立,即a=b时,a+b=2$\sqrt{m}$,∴当a=b=$\sqrt{m}$时,a+b取得最小值(填“最大”或“最小”). 如图,四边形ABCD是矩形,C在x轴上,A(-1,0),B(0,2),双曲线y=$\frac{k}{x}$经过点D,则k的值为-6.
如图,四边形ABCD是矩形,C在x轴上,A(-1,0),B(0,2),双曲线y=$\frac{k}{x}$经过点D,则k的值为-6.