题目内容
一元二次方程2x2-5x=-4的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
考点:根的判别式
专题:
分析:先求出△的值,再根据△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数;△<0?方程没有实数根,进行判断即可.
解答:解:∵2x2-5x=-4,
∴2x2-5x+4=0,
∵△=(-5)2-4×2×4=-7<0,
∴一元二次方程2x2-5x=-4无实数根;
故选C.
∴2x2-5x+4=0,
∵△=(-5)2-4×2×4=-7<0,
∴一元二次方程2x2-5x=-4无实数根;
故选C.
点评:此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
下列语句中,正确的是( )
| A、两个有理数的差一定小于被减数 |
| B、两个有理数的和一定比这两个有理数的差大 |
| C、绝对值相等的两数之差为零 |
| D、零减去一个有理数等于这个有理数的相反数 |
若二次函数y=(m-1)x2+(m2+3m-4)x-2的对称轴为y轴,则m的值是( )
| A、-1或4 | B、-4 |
| C、1或-4 | D、-1 |
关于x的方程kx2-4x-3=0有实数根,则k的值等于( )
A、k=0或k=-
| ||
B、k≥-
| ||
C、k≥-
| ||
D、k≥-
|
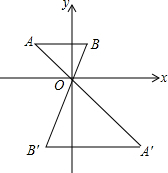 如图,△OAB和△OA′B′是相似比为1:3的位似图形,点O为位似中心.若△OAB内点P(x,y)与△OA′B′内一点P′是一对对应点,则点P的坐标为
如图,△OAB和△OA′B′是相似比为1:3的位似图形,点O为位似中心.若△OAB内点P(x,y)与△OA′B′内一点P′是一对对应点,则点P的坐标为