题目内容
19.已知关于x的方程kx2-(k+2)x+2=0(k≠0).(1)求证:无论k为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数k的值.
分析 (1)证明根的判别式△不小于0即可;
(2)先把方程因式分解,用k表示出方程的根,再根据方程的两个实数根都是整数,进而求出k的值.
解答 解:(1)△=(k+2)2-8k=(k-2)2≥0,
即无论k为何值时,这个方程总有两个实数根;
(2)∵kx2-(k+2)x+2=0,
∴(kx-2)(x-1)=0,
∴x1=$\frac{2}{k}$,x2=1,
∵方程的两个实数根都是整数,
∴k=1或2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.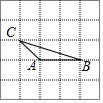 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
9.利用图象求得方程x2-x-1=0的近似根为( )
| A. | x1=1.6,x2=0.6 | B. | x1=-1.6,x2=0.6 | C. | x1=1.6,x2=-0.6 | D. | x1=-1.6,x2=-0.6 |
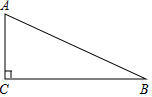 已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
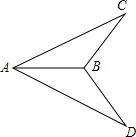 如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.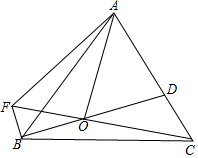 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.