题目内容
7.新定义[a,b]为一次函数(其中a≠0,且a,b为实数)的“关联数”,若“关联数”[3,m+2]所对应的一次函数是正比例函数,则关于x的方程$\frac{1}{x-1}$+$\frac{1}{m}$=1的解为$\frac{5}{3}$.分析 根据题中的新定义求出m的值,确定出分式方程,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:根据“关联数”[3,m+2]所对应的一次函数是正比例函数,
得到y=3x+m+2为正比例函数,即m+2=0,
解得:m=-2,
则分式方程为$\frac{1}{x-1}$-$\frac{1}{2}$=1,
去分母得:2-(x-1)=2(x-1),
去括号得:2-x+1=2x-2,
解得:x=$\frac{5}{3}$,
经检验x=$\frac{5}{3}$是分式方程的解.
故答案为:x=$\frac{5}{3}$.
点评 此题考查了一次函数的定义,解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.熟练掌握题中的新定义是解本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
15.下列命题中:①4的平方根是±2;②16的算术平方根是2;③若x2=9,则x=3;④若x3=-8,则x=-2.其中是真命题的有( )
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
12.正方形和下列边长相同的正多边形地砖组合中,不能够铺满地面的是( )
| A. | 正三角形 | B. | 正六边形 | ||
| C. | 正八边形 | D. | 正三角形和正六边形 |
16.正五边形的一个内角的度数为( )
| A. | 100° | B. | 108° | C. | 112° | D. | 120° |
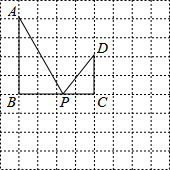 在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.
在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.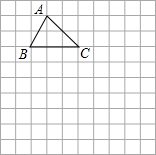 在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)
在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)