题目内容
12.正方形和下列边长相同的正多边形地砖组合中,不能够铺满地面的是( )| A. | 正三角形 | B. | 正六边形 | ||
| C. | 正八边形 | D. | 正三角形和正六边形 |
分析 正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满
解答 解:A、正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面;
B、正方形的每个内角是90°,正六边形的每个内角是120°,90°m+120°n=360°,m=4-$\frac{4}{3}$n,显然n取任何整数时,m不能得正整数,故不能铺满;
C、正方形的每个内角是90°,正八边形的每个内角是135°,∵90°+2×135°=360°,∴能铺满地面;
D、正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120度,∵60°+2×90°+120°=360°,∴能铺满地面.
故选:B.
点评 本题主要考查了平面几何图形镶嵌,解题的关键是明确围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.

练习册系列答案
相关题目
4. 如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
 如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
3.下列命题中是假命题的是( )
| A. | △ABC中,若∠A=∠C-∠B,则△ABC是直角三角形 | |
| B. | △ABC中,若a2=b2-c2,则△ABC是直角三角形 | |
| C. | △ABC中,若a:b:c=5:12:13,则△ABC是直角三角形 | |
| D. | △ABC中,若∠A,∠B,∠C的度数比是3:4:5,则△ABC是直角三角形 |
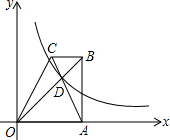 如图,已知四边形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC,BO相交于点D,反比例函数y=$\frac{k}{x}$经过点D.若△BCD的面积为3,△OCD的面积为6,则反比例函数的解析式为y=$\frac{16}{x}$.
如图,已知四边形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC,BO相交于点D,反比例函数y=$\frac{k}{x}$经过点D.若△BCD的面积为3,△OCD的面积为6,则反比例函数的解析式为y=$\frac{16}{x}$.