题目内容
20.已知△ABC是等腰直角三角形,∠BAC=90°,AB=AC,点D是边BC上的一个动点(不运动至点B,C),点E在BC所在直线上,连结AD,AE,且∠DAE=45°(1)若点E是线段BC上一点,如图1,作点D关于直线AE的对称点F,连结AF,CF,DF,EF
①求证:△ABD≌△ACF;
②若BD=1,DE=2,求CE的长;
(2)如图2,若BD=$\frac{8}{5}$,AB=$\sqrt{2}$,求CE的长.(直接写出答案即可)
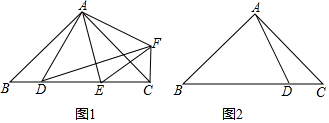
分析 (1)①根据轴对称的性质,得到AD=AF,∠DAE=∠FAE=45°,再根据同角的余角相等,得到∠BAD=∠FAC,即可判定△ABD≌△ACF(SAS);
②由①可得:△ABD≌△ACF,据此得出∠B=∠ACF=45°,BD=CF=1,进而得到∠ECF=∠ACB+∠ACF=90°,再根据DE=EF=2,运用勾股定理求得CE即可;
(2)分两种情况进行讨论:当点E在BC延长线上时,作点D关于直线AE的对称点F,连结AF,CF,EF;当点E在线段BC上时,作点D关于直线AE的对称点F,连结AF,BF,EF.分别根据全等三角形的性质以及勾股定理,求得CE的长即可.
解答 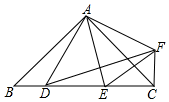 解:(1)①∵点D与点F关于直线AE的对称,
解:(1)①∵点D与点F关于直线AE的对称,
∴AE垂直平分DF,
∴AD=AF,
∴∠DAE=∠FAE=45°,
即∠DAF=90°,
∴∠DAC+∠FAC=90°,
∵∠BAC=90°,
∴∠DAC+∠BAD=90°,
∴∠BAD=∠FAC,
在△ABD与△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACF(SAS);
②由①可得:△ABD≌△ACF,
∴∠B=∠ACF=45°,BD=CF=1,
∴∠ECF=∠ACB+∠ACF=90°,
∵AE垂直平分DF,
∴DE=EF=2,
∴CE=$\sqrt{E{F}^{2}-C{F}^{2}}$=$\sqrt{3}$;
(2)CE=3或$\frac{5}{4}$.
理由:如图所示,当点E在BC延长线上时,作点D关于直线AE的对称点F,连结AF,CF,EF,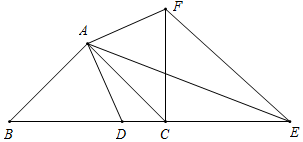
根据△ABD≌△ACF,可得BD=CF=$\frac{8}{5}$,
在等腰直角三角形ABC中,AB=$\sqrt{2}$,
∴BC=2,
∴CD=$\frac{2}{5}$,
∴DE=CE+$\frac{2}{5}$=EF,
在Rt△CEF中,CE2+($\frac{8}{5}$)2=(CE+$\frac{2}{5}$)2,
解得CE=3;
如图所示,当点E在线段BC上时,作点D关于直线AE的对称点F,连结AF,BF,EF,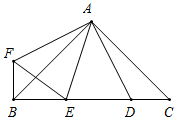
根据△ABF≌△ACD,可得BF=CD=$\frac{2}{5}$,
∴DE=CE-$\frac{2}{5}$=EF,
又∵BE=BC-CE=2-CE,
∴在Rt△BEF中,($\frac{2}{5}$)2+(2-CE)2=(CE-$\frac{2}{5}$)2,
解得CE=$\frac{5}{4}$.
点评 本题属于三角形综合题,主要考查了全等三角形的性质以判定,等腰直角三角形的性质,勾股定理以及对称轴的性质的综合应用,解决问题的关键是掌握全等三角形的判定方法,解题时注意分类思想的运用.

| 甲 | 乙 | 丙 | |
| $\overline{x}$ | 8 | 9 | |
| s2 | 1 | 1.2 |
| A. | $\overline x=8$,S2=0.7 | B. | $\overline x=8$,S2=1.2 | C. | $\overline x=9$,S2=1 | D. | $\overline x=9$,S2=1.5 |
| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )
如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是( )| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
| A. |  长方体 | B. |  正方体 | C. |  圆柱体 | D. |  三棱锥 |
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )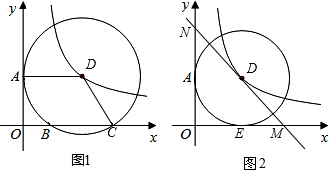
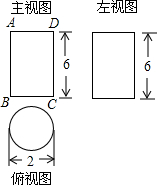 一个几何体的三视图如图所示,如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到CD的中点E,请你求出这个线路的最短路径.
一个几何体的三视图如图所示,如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到CD的中点E,请你求出这个线路的最短路径.