题目内容
19.平面直角坐标系中,已知P1的坐标为(1,0),将其绕着原点按逆时针方向旋转30°得到点P2,延长OP2到P3,使OP3=2OP2,再将点P3绕着原点按逆时针方向旋转30°得到点P4,延长OP4到P5,使OP5=2OP4,如此继续下去,则点P2012的坐标是(${2}^{1006}\sqrt{3}$,-21005).分析 解题的关键是抓住旋转的三要素:旋转中心原点,旋转方向逆时针,旋转角度30°,总结规律寻找得P2012的坐标.
解答 解:根据旋转的特点,总结规律.
P1(1,0)在x轴上,P2($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),P3($\sqrt{3}$,1),P4(1,$\sqrt{3}$),P5(2,2$\sqrt{3}$),P6(0,4),P7(0,8)在y轴上,
照此规律,每经过6个点就落到坐标轴上,2012÷6=335…2,335除以4,余数是3,
故点P2012的位置在第四象限,
∴P2012的坐标是(${2}^{1006}\sqrt{3}$,-21005).
故答案为:(${2}^{1006}\sqrt{3}$,-21005)
点评 本题主要考查对坐标与图形变换-旋转等知识点的理解和掌握,解决本题的关键是通过作图,分析,观察,得到相应的规律.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
11.已知点A的坐标为(-2,3),点B的坐标为(0,1),则点A关于点B对称点的坐标为( )
| A. | (-2,2) | B. | (2,-3) | C. | (2,-1) | D. | (2,3) |
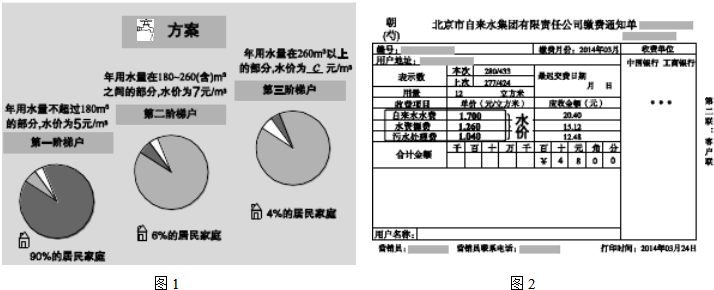
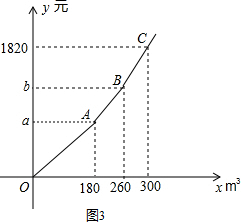
 如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.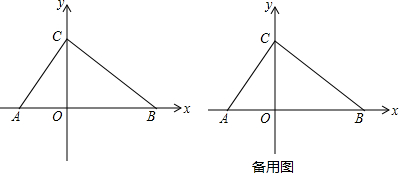
 如图所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b,BC边上的高AD=h.(要求:写出作法,并保留作图痕迹)
如图所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b,BC边上的高AD=h.(要求:写出作法,并保留作图痕迹) 如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.
如图,在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x米,面积为y平方米.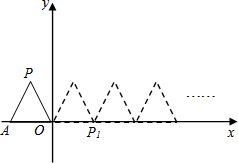 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标为2012.5.
如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标为2012.5.