题目内容
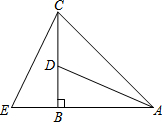 如图,在△ABC中,∠ABC=90°,AB=BC,点D在边BC上,点E在AB的延长线上,且BE=BD.
如图,在△ABC中,∠ABC=90°,AB=BC,点D在边BC上,点E在AB的延长线上,且BE=BD.(1)求证:△ABD≌△CBE;
(2)若∠BAD=20°,求∠ACE的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)直接运用SAS公理,即可解决问题.
(2)证明∠BCE=∠BAD=20°;证明∠ACB=45°,即可解决问题.
(2)证明∠BCE=∠BAD=20°;证明∠ACB=45°,即可解决问题.
解答:解:(1)如图,
在△ABD与△CBE中,
CBE,
∴△ABD≌△CBE(SAS).
(2)∵△ABD≌△CBE,
∴∠BCE=∠BAD=20°;
∵∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴∠ACE=65°.

在△ABD与△CBE中,
|
∴△ABD≌△CBE(SAS).
(2)∵△ABD≌△CBE,
∴∠BCE=∠BAD=20°;
∵∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴∠ACE=65°.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是牢固掌握全等三角形的判定定理及其性质定理的内容,并能灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
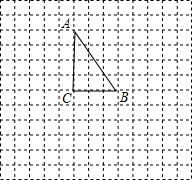 如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.
如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度. 如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=
如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=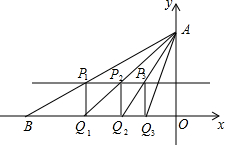 已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为
已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为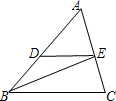 如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平分线,交AB于点E,请判断△BDE的形状,并说明理由.
如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平分线,交AB于点E,请判断△BDE的形状,并说明理由. 如图,已知AB∥CD,P为BC上一点,试说明当点P在BC上移动时,总有∠α+∠β=∠B.
如图,已知AB∥CD,P为BC上一点,试说明当点P在BC上移动时,总有∠α+∠β=∠B. 如图,在△ABC中,点D在BC边上,且AB=AC=BD,∠CAD=25°,求∠BAC的度数.
如图,在△ABC中,点D在BC边上,且AB=AC=BD,∠CAD=25°,求∠BAC的度数.