题目内容
17.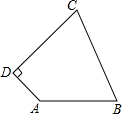 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
分析 连接AC,过点C作CE⊥AB于点E,在Rt△ACD中根据勾股定理求出AC的长,由等腰三角形的性质得出AE=BE=$\frac{1}{2}$AB,在Rt△CAE中根据勾股定理求出CE的长,再由S四边形ABCD=S△DAC+S△ABC即可得出结论.
解答 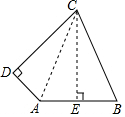 解:连接AC,过点C作CE⊥AB于点E.
解:连接AC,过点C作CE⊥AB于点E.
∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,
AC=$\sqrt{A{D^2}+C{D^2}}=\sqrt{{5^2}+{{12}^2}}=13$.
∵BC=13,
∴AC=BC.
∵CE⊥AB,AB=10,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}×10=5$.
在Rt△CAE中,
CE=$\sqrt{A{C^2}-A{E^2}}=\sqrt{{{13}^2}-{5^2}}=12$.
∴S四边形ABCD=S△DAC+S△ABC=$\frac{1}{2}×5×12+\frac{1}{2}×10×12=30+60=90$.
点评 本题考查的是勾股定理及三角形的面积公式,等腰三角形的判定和性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中, 一个大正方形和四个全等的小正方形按图①、图②两种方式摆放,根据图中数据,则图②的大正方形中未被小正方形覆盖部分的面积大小为24.
一个大正方形和四个全等的小正方形按图①、图②两种方式摆放,根据图中数据,则图②的大正方形中未被小正方形覆盖部分的面积大小为24.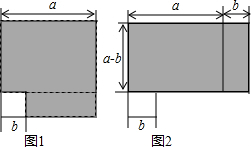 如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:a2-b2=(a+b)(a-b).
如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:a2-b2=(a+b)(a-b). 如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.
如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.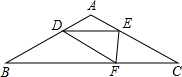 如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.
如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.


