题目内容
1. 如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线.
如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线.
分析 根据SAS证明△ADF≌△CDF,再根据全等三角形的性质证明即可.
解答 证明:∵DF是∠ADC的平分线,
∴∠CDF=∠ADF.
又∵AD=DC,DF=DF,
在△ADF与△CDF中,
$\left\{\begin{array}{l}{AD=DC}\\{∠CDF=∠ADF}\\{DF=DF}\end{array}\right.$,
∴△ADF≌△CDF,
∴AF=CF,
∴∠ACF=∠CAF.
∵AF∥CB,°
∴∠CAF=∠ACB,
∴∠ACF=∠ACB,即CA平分∠BCF
点评 此题主要考查学生对全等三角形的判定与性质以及平行线的性质,角平分线的理解和掌握,关键是根据SAS证明△ADF≌△CDF.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.如果a、b、c是一个直角三角形的三边,则a:b:c可以等于( )
| A. | 1:2:4 | B. | 2:3:4 | C. | 3:4:7 | D. | 5:12:13 |
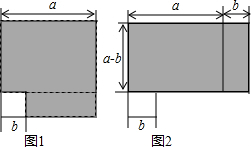 如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:a2-b2=(a+b)(a-b).
如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:a2-b2=(a+b)(a-b).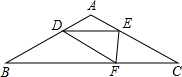 如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.
如图,在△ABC中,AB=AC=15,∠B=30°,点D为AB边上一动点,且AD=AE,BD=DF,要使△DEF与△CEF均为直角三角形,则AD的值为5或6.