题目内容
2.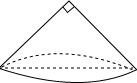 如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为2$\sqrt{2}$π.(结果保留π)
如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为2$\sqrt{2}$π.(结果保留π)
分析 根据圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长计算扇形的面积即圆锥的侧面积.
解答 解:∵直角边长为2,
∴斜边长为2$\sqrt{2}$,
则底面圆的面积为2$\sqrt{2}π$,
则这个圆锥的侧面积为:$\frac{1}{2}$×2×2$\sqrt{2}π$=2$\sqrt{2}π$,
故答案为:2$\sqrt{2}π$.
点评 本题考查的是圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
10.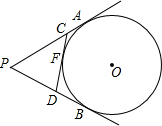 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则$\frac{OA}{PA}$的值是( )| A. | $\frac{2}{13}\sqrt{13}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
7.-2013的相反数是( )
| A. | -$\frac{1}{2013}$ | B. | $\frac{1}{2013}$ | C. | -2013 | D. | 2013 |
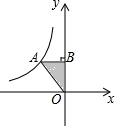 如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.
如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.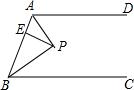 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )