题目内容
12．
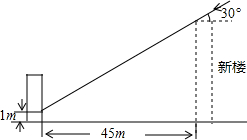为了解决楼房之间的采光问题，某市有关部门规定：两幢楼房之间的最小距离要使中午12时不能遮光．如图，旧楼的一楼窗台高1m，现计划在旧楼正南方45m处建一幢新楼．已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°，问新楼房最高可建多少米？
分析 过点D作DE⊥AB，可得四边形BCDE是矩形，知BC=DE=45m，CD=BE=1m，在RT△ADE中AE=tan30°•DE求出AE的长，由AB=AE+EB可得答案．
解答 解：如图，过点D作DE⊥AB与点E，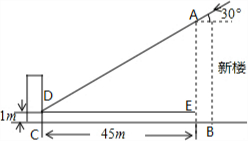
在RT△ADE中，∠ADE=30°，DE=BC=45m，
则AE=tan30°•DE=$\frac{\sqrt{3}}{3}$×45=15$\sqrt{3}$，
而EB=DC=1m，
∴AB=AE+EB=15$\sqrt{3}$+1，
答：新楼房最高可建（15$\sqrt{3}$+1）米．
点评 此题考查了解直角三角形的应用．注意能根据题意构造直角三角形，并能借助于解直角三角形的知识求解是解此题的关键．
练习册系列答案
相关题目
2．计算3-（-6）的结果等于（ ）
| A． | -9 | B． | -3 | C． | 3 | D． | 9 |
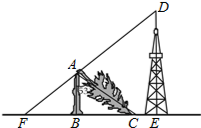如图，一棵大树在一次强台风中折断倒下，未折断树杆AB与地面仍保持垂直的关系，而折断部分AC与未折断树杆AB形成60°的夹角．树杆AB旁有一座与地面垂直的铁塔DE，测得BE=6米，塔高DE=9米．在某一时刻的太阳照射下，未折断树杆AB落在地面的影子FB长为4米，且点F、B、C、E在同一条直线上，点F、A、D也在同一条直线上．求这棵大树没有折断前的高度．
如图，一条光纤线路从A地到B地需要经过C地，图中AC=40千米，