题目内容
16.如图,四边形ABCD是矩形,AB=3,BC=8,E是AD的中点,作射线BE,点M、N同时从点B出发,点M以每秒4个单位长度的速度沿射线BE方向运动,点N以每秒5个单位长度的速度沿射线BC方向运动.设运动时间为t秒(t>0).
(1)连接MN,判断直线MN与直线BE的位置关系,并说明理由;
(2)当点M与点E重合时,t=$\frac{5}{4}$秒;当直线MN经过点D时,t=$\frac{41}{20}$秒;
(3)在直线MN没有经过点D之前,设△BMN与矩形ABCD重叠部分的面积为S,求S与t的函数关系式.
分析 (1)在△ABE中,由勾股定理可知BE=5,从而得到cos∠AEB=$\frac{4}{5}$,然后由MB=4t,BN=5t,可知$\frac{MB}{NB}$=cos∠EBN,于是得到MN⊥MB;
(2)当点M与点E重合时,BE=4t=5,从而可求得t=$\frac{5}{4}$,当点直线MN经过点D时,BM=BE+ME=5+$\frac{16}{5}$=$\frac{41}{5}$,由4t=$\frac{41}{5}$可求得t=$\frac{41}{20}$;
(3)如图2所示;当0<t≤$\frac{5}{4}$时,△BMN与矩形ABCD重叠部分的面积等于△BMN的面积;如图3所示,当$\frac{5}{4}<t≤$$\frac{8}{5}$时,S=S△BNM-S△EFM,如图4所示当$\frac{8}{5}<t≤\frac{41}{20}$时,S=梯形EDCB的面积-△DFG的面积.
解答 解:(1)MN⊥BE.
理由:∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC.
∵E是AD的中点,
∴AE=4.
在Rt△ABE中,由勾股定理可知:BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=5.
∴cos∠AEB=$\frac{AE}{BE}$=$\frac{4}{5}$.
∵AE∥BC,
∴∠EBN=∠AEB.
∴cos∠EBC=$\frac{4}{5}$.
∵MB=4t,BN=5t,
∴$\frac{MB}{BN}$=$\frac{4}{5}$.
∴$\frac{MB}{BN}=cos∠EBN$.
∴MN⊥BE.
(2)当点M与点E重合时,BE=4t=5,解得:t=$\frac{5}{4}$.
当直线MN经过点D时,如图1所示:
∵E是AD的中点,
∴DE=$\frac{1}{2}AD$=$\frac{1}{2}×8$=4.
∵∠MED=∠AEB,
∴ME=ED×$\frac{4}{5}$=$\frac{16}{5}$.
∴MB=BE+ME=5+$\frac{16}{5}$=$\frac{41}{5}$.
∴4t=$\frac{41}{5}$.
解得:t=$\frac{41}{20}$.
故答案为:$\frac{5}{4}$;$\frac{41}{20}$.
(3)如图2所示:当0<t$≤\frac{5}{4}$时.
在Rt△BNM中,MN=$\sqrt{N{B}^{2}-B{M}^{2}}$=3t.
∴S=S△BMN=$\frac{1}{2}NM•BM$=$\frac{1}{2}×3t×4t$=6t2.
如图3所示:当$\frac{5}{4}<t≤\frac{8}{5}$时.
∵EM=4t-5,
∴MF=$\frac{3}{4}(4t-5)$.
S=S△BNM-S△EFM=6t2-$\frac{3}{8}(4t-5)^{2}$=15t-$\frac{75}{8}$;
如图4所示:当$\frac{8}{5}<t<\frac{41}{20}$时.
∵CN=BN-BC=5t-8.
∴CG=$\frac{4}{3}$CN=$\frac{4}{3}×(5t-8)$=$\frac{20t}{3}-\frac{32}{3}$.
∴DG=DC-CG=$\frac{41}{3}-\frac{20t}{3}$.
∴DF=$\frac{3}{4}DG$.
∴S△DFG=$\frac{1}{2}×DF•DG$=$\frac{1}{2}×\frac{3}{4}×(\frac{1}{3})^{2}(41-20t)^{2}$=$\frac{50}{3}{t}^{2}-\frac{205}{3}t+\frac{1681}{24}$.
∵S=梯形EDCB的面积-△DFG的面积=$\frac{1}{2}×(4+8)×3$-($\frac{50}{3}{t}^{2}-\frac{205}{3}t+\frac{1681}{24}$)
=-${\frac{50}{3}t}^{3}+\frac{205}{3}t$-$\frac{1249}{24}$.
综上所述,S与t的函数关系式为s=$\left\{\begin{array}{l}{6{t}^{2}(0<t≤\frac{5}{4})}\\{15t-\frac{75}{8}(\frac{5}{4}<t≤\frac{8}{5})}\\{-\frac{50}{3}{t}^{3}+\frac{205}{3}t-\frac{1249}{24}(\frac{8}{5}<t<\frac{41}{20})}\end{array}\right.$.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了矩形的性质、勾股定理、锐角三角函数的定义、三角形的面积公式、梯形的面积公式,根据题意画出符合图形的图形,然后依据锐角三角函数的定义、三角形的面积公式、梯形的面积公式求得S与t的函数关系是解题的关键.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | 1 | B. | 0 | C. | 0或1 | D. | 0或-1 |
| A. | 5x2y3 | B. | -2x4y2 | C. | 7 | D. | 3x5y |

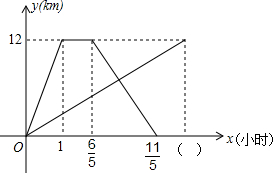 一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:
一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题: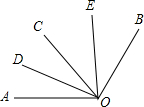 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.