题目内容
2.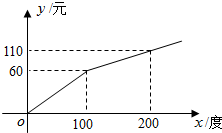 电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.
电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.(1)月用电量为100度时,应交电费60元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为250度时,应交电费多少元?
分析 (1)根据函数图象,当x=100时,可直接从函数图象上读出y的值;
(2)设一次函数为:y=kx+b,将(100,60),(200,110)两点代入进行求解即可;
(3)将x=250代入(2)式所求的函数关系式进行求解可得出应交付的电费.
解答 解:(1)根据函数图象,知:当x=100时,y=60,故当月用电量为100时,应交付电费60元;
故答案为:60
(2)设一次函数为y=kx+b,当x=100时,y=60;当x=200时,y=110
∴$\left\{\begin{array}{l}{100k+b=60}\\{200k+b=110}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.5}\\{b=10}\end{array}\right.$,
所求的函数关系式为:y=0.5x+10(x≥100)
(3)当x=250时,y=0.5×250+10=135,
∴月用量为250度时,应交电费135元.
点评 本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.

练习册系列答案
相关题目
13.若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a-b+c=0,则方程的根是( )
| A. | 1,0 | B. | -1,0 | C. | 1,-1 | D. | 无法确定 |
17.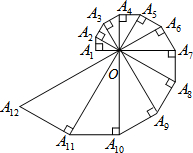 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )| A. | 22013 | B. | 22014 | C. | ($\frac{2}{\sqrt{3}}$)2013 | D. | ($\frac{2}{\sqrt{3}}$)2014 |
11.已知:$\frac{M}{x+2}$+$\frac{n}{x-3}$=$\frac{5x}{(x+2)(x-3)}$,求M、N的值( )
| A. | M=2,N=3 | B. | M=3,N=2 | C. | M=2,N=2 | D. | M=3,N=3 |
 如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$.
如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$.