Question

4．如图，已知正方形ABCD的边长为$\sqrt{10}$，对角线AC、BD交于点O，点E在BC上，且CE=2BE，过B点作BF⊥AE于点F，连接OF，则线段OF的长度为$\sqrt{2}$．

Answer 1

分析 先判断出∠OBF=∠CAE，从而得出△AOG≌△BOF，即可判断出△OFG是等腰直角三角形，再根据勾股定理和射影定理求出BF，AF，AG，即可得出FG．

解答 解：如图，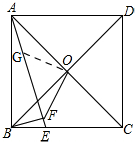

作OG⊥OF交AE于G，
∴OA=OB，∠FOG=90°，
∵AC，BD是正方形的对角线，
∴∠AOB=90°，
∴∠AOG=∠BOF，
∵BF⊥AE，
∴∠BAE+∠ABF=90°，
∵∠BAE=∠BAC-∠CAE
∴∠OBF=∠ABF-∠ABD=90°-∠BAE-∠ABD=90°-∠BAC+∠CAE-∠ABD=∠CAE，
在△AOG和△BOF中，
$\left\{\begin{array}{l}{∠CAE=∠OBF}\\{OA=OB}\\{∠AOG=∠BOF}\end{array}\right.$
∴△AOG≌△BOF，
∴OG=OF，
∴△OFG是等腰直角三角形，
∵CE=2BE，BC=$\sqrt{10}$，
∴BE=$\frac{\sqrt{10}}{3}$，
根据勾股定理得，AE=$\frac{10}{3}$，
在Rt△ABE中，
根据射影定理得，BF=1，AF=3，
∴AG=BF=1，
GF=AF-BF=2，
∴OF=$\sqrt{2}$．
故答案为$\sqrt{2}$．

点评 本题考查了全等三角形的判定和性质，直角三角形的判定以及射影定理、勾股定理的应用，作出适当的辅助线，构建全等三角形是解答此题的关键．